วันนี้ ค้นไปพบกระทู้แปะบทความ เรื่อง Twin Paradox
เป็นบทความ ที่น่าจะแปลและเรียบเรียง มาจากส่วนหนึ่งของวิกิพีเดีย
เขียนได้ละเอียดดี ผมก็เลยได้อ่านอีกรอบจนจบ
ตอนอ่านในวิกิภาษาอังกฤษ มันหนักหัวนิดๆ จึงไม่ได้คิดอะไรต่อ
แต่มาอ่านเที่ยวนี้ ก็เลยพบว่า
คำอธิบายนั้น เป้นแบบมีธงอยู่ (น่าจะโดยไม่รู้ตัว )
อ้างอิง
https://ppantip.com/topic/33435007
ผมขอยกข้อความจากกระทู้เฉพาะส่วนที่เป็นคำอธิบาย ดังนี้
มุมมองของขาว (‘เฝ้าบ้าน’)
มุมมองของเขียว (‘ท่องเที่ยวไป’)
ขาวจะบอกว่า เขียวต้องใช้เวลาเดินทางไปถึงที่หมาย Dt1= L/v = (4 ปีแสง)/(0.8 c) = 5 ปี
และใช้เวลาเดินทางกลับเท่าๆ กัน นั่นคือ Dt2 = 5 ปี
รวมเวลาที่ขาวต้องรอเขียวกลับมายังโลก Dt1 + Dt2= 5 ปี + 5 ปี = 10 ปี
นั่นคือ ขาวต้องรอถึง 10 ปี กว่าจะพบกับเขียว
เขียวบอกว่าระยะทางขาไปนั้น จะหดสั้นเหลือแค่ L' = L/k = (4 ปีแสง)/(5/3) = 12/5 ปีแสง = 2.4 ปีแสง
และเนื่องจากเขียวเดินทางด้วยอัตราเร็ว v=0.8c
ดังนั้น เขาจะถึงที่หมายในเวลา Dt'1 = L'/v = (2.4 ปีแสง)/(0.8 c) = 3 ปี
โดยขากลับ
(แม้จะอยู่ในอีกกรอบหนึ่ง) ก็จะใช้เวลาเท่ากัน คือ Dt'2= 3 ปี
รวมเวลาในการเดินทางของเขียวทั้งหมด Dt'1 + Dt'2 3 ปี + 3 ปี = 6 ปี
นั่นคือ เวลาของเขียวผ่านไปเพียง 6 ปี ก็พบกับขาวแล้ว
เพื่อให้เห็นเหตุการณ์ชัดเจนขึ้น สมมติว่า แต่ละคนส่งสัญญานคลื่นแม่เหล็กไฟฟ้า (เช่น สัญญาณวิทยุ)
กลับไปหาอีกฝ่ายปีละ 1 ครั้ง คำถามก็คือ แต่ละฝ่ายจะได้รับสัญญาณกี่ครั้ง? เมื่อไรบ้าง?
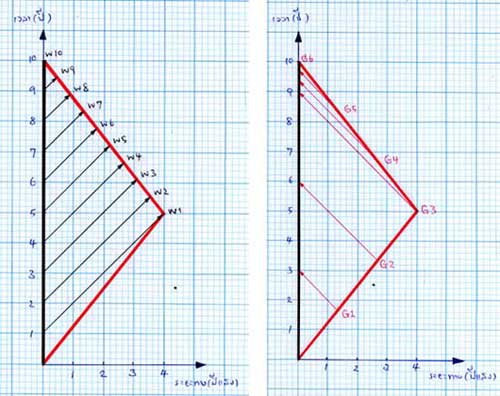
ภาพที่ 4 เป็นแผนภาพกาลอวกาศจากมุมมองของขาวซึ่งน่าจะช่วยให้เห็นเหตุการณ์นี้ชัดเจนขึ้น
โดยสัญญาณที่ขาวส่งไประบุด้วยตัวอักษร W (แทนคำว่า White = ขาว) ตามด้วยตัวเลขของปีที่ส่ง เช่น W1
คือ สัญญาณที่ขาวส่งไปหาเขียวเมื่อสิ้นปีที่ 1 ของขาว เป็นต้น
ส่วนสัญญาณจากเขียวจะขึ้นต้นด้วยตัวอักษร G (แทนคำว่า Green = เขียว) ตามด้วยปีที่ส่งเช่นเดียวกัน เช่น G3
คือ สัญญาณที่เขียวส่งไปหาขาวเมื่อสิ้นปีที่ 3 ของเขียว เป็นต้น
ภาพที่ 4 (ซ้าย) แสดงสัญญาณที่ขาวส่งไปหาเขียว
จะเห็นว่าเขียวจะได้รับสัญญาณ W1 ตอนที่เดินทางไปถึงจุดหมายปลายทางพอดี
นั่นคือ เมื่อเวลาของขาวผ่านไป 5 ปี ในขณะที่เวลาของเขียวผ่านไปเพียง 3 ปี
(ผู้อ่านอาจลองคำนวณเพื่อตรวจสอบดูเอง)
ส่วนสัญญาณที่เหลือในปีที่ 2 (W2) ถึงปีที่ 10 (W10) นั้น เขียวจะได้รับแบบถี่ยิบในช่วงขากลับ
โดยครั้งสุดท้ายได้รับในปีที่ 6 ของเขียว (เท่ากับปีที่ 10 ของขาว) ตอนพบกันอีกครั้งหนึ่งพอดี
เมื่อเขียวได้รับสัญญาณ W1 ถึง W10 จากขาว รวม 10 ครั้ง เขียวย่อมระบุได้ว่า ขาวแก่เพิ่มขึ้น 10 ปี
ในทำนองเดียวกัน หากพิจารณาภาพที่ 4(ขวา) ซึ่งแสดงสัญญาณที่เขียวส่งไปหาขาว
จะเห็นว่าขาวได้รับสัญญาณจากเขียวทั้งสิ้น 6 ครั้ง ดังนั้นขาวย่อมสรุปจากหลักฐานนี้ว่าเขียวแก่เพิ่มขึ้นเพียง 6 ปี
นั่นคือ ตามทฤษฎีสัมพัทธภาพพิเศษ เขียวจึงแก่ช้ากว่าขาวเช่นกัน!
----------------------------------------------------------------------------------------
คำอธิบายนี้ เป็นการพูดด้านเดียว คือฝ่ายนายเขียว เดินทาง และใช้เวลาน้อยลง
ไม่มีการพูดถึง เวลาของนายขาวเลย
เป็นการตัดเหตการณ์เหลือข้างเดียว
จึง ไม่เป็น Paradox
อ่านจบ ถ้าเรายัง งงๆ
ก็จะเข้าใจไปว่า คำอธิบายสมบูรณ์แล้ว
สรุปว่า ผู้เดินทางมีเวลาลดลงจริง ซะงั้น
ที่เรียกว่า เป็นการอธิบายแบบปักธงไว้ก่อน
ก็เพราะ ผู้อธิบาย มีความเชื่อว่า นายเขียวเป็นผู้เดินทางไป เปลี่ยนเฟรม และกลับ
การเชื่อเช่นนี้ เพราะผู้อธิบายเคยชินกับ สภาพนิ่งของโลก และจักรวาล
จึงเห็นว่า นายเขียวเดินทางไปกับยานและมีความเร็ว (แต่นายขาวไม่มีความเร็ว)
เป็นผลให้ เวลาของนายเขียวช้าลง
(และลืมมองตามโจทย์Paradox ว่านายเขียวเห็นนายขาวมีความเร็วด้วย)
โดยสรุป คำอธิบาย กลับกลายเป้นการอธิบายการเคลื่อนที่สัมบูรณ์
โดยมีโลก เป็นจุดอ้างอิงสัมบูรณ์
ซึ่ง หากผลของเวลายืดช้าลง เป็นฝ่ายนายเขียวจริง
ก็เท่ากับว่า ต้องพิจารณาเรื่อง จุดอ้างอิงสัมบูรณ์แล้ว
Twin Paradox คำเฉลย ที่ยังมีข้อผิดพลาด
เป็นบทความ ที่น่าจะแปลและเรียบเรียง มาจากส่วนหนึ่งของวิกิพีเดีย
เขียนได้ละเอียดดี ผมก็เลยได้อ่านอีกรอบจนจบ
ตอนอ่านในวิกิภาษาอังกฤษ มันหนักหัวนิดๆ จึงไม่ได้คิดอะไรต่อ
แต่มาอ่านเที่ยวนี้ ก็เลยพบว่า
คำอธิบายนั้น เป้นแบบมีธงอยู่ (น่าจะโดยไม่รู้ตัว )
อ้างอิง https://ppantip.com/topic/33435007
ผมขอยกข้อความจากกระทู้เฉพาะส่วนที่เป็นคำอธิบาย ดังนี้
มุมมองของขาว (‘เฝ้าบ้าน’)
มุมมองของเขียว (‘ท่องเที่ยวไป’)
ขาวจะบอกว่า เขียวต้องใช้เวลาเดินทางไปถึงที่หมาย Dt1= L/v = (4 ปีแสง)/(0.8 c) = 5 ปี
และใช้เวลาเดินทางกลับเท่าๆ กัน นั่นคือ Dt2 = 5 ปี
รวมเวลาที่ขาวต้องรอเขียวกลับมายังโลก Dt1 + Dt2= 5 ปี + 5 ปี = 10 ปี
นั่นคือ ขาวต้องรอถึง 10 ปี กว่าจะพบกับเขียว
เขียวบอกว่าระยะทางขาไปนั้น จะหดสั้นเหลือแค่ L' = L/k = (4 ปีแสง)/(5/3) = 12/5 ปีแสง = 2.4 ปีแสง
และเนื่องจากเขียวเดินทางด้วยอัตราเร็ว v=0.8c
ดังนั้น เขาจะถึงที่หมายในเวลา Dt'1 = L'/v = (2.4 ปีแสง)/(0.8 c) = 3 ปี
โดยขากลับ (แม้จะอยู่ในอีกกรอบหนึ่ง) ก็จะใช้เวลาเท่ากัน คือ Dt'2= 3 ปี
รวมเวลาในการเดินทางของเขียวทั้งหมด Dt'1 + Dt'2 3 ปี + 3 ปี = 6 ปี
นั่นคือ เวลาของเขียวผ่านไปเพียง 6 ปี ก็พบกับขาวแล้ว
เพื่อให้เห็นเหตุการณ์ชัดเจนขึ้น สมมติว่า แต่ละคนส่งสัญญานคลื่นแม่เหล็กไฟฟ้า (เช่น สัญญาณวิทยุ)
กลับไปหาอีกฝ่ายปีละ 1 ครั้ง คำถามก็คือ แต่ละฝ่ายจะได้รับสัญญาณกี่ครั้ง? เมื่อไรบ้าง?
ภาพที่ 4 เป็นแผนภาพกาลอวกาศจากมุมมองของขาวซึ่งน่าจะช่วยให้เห็นเหตุการณ์นี้ชัดเจนขึ้น
โดยสัญญาณที่ขาวส่งไประบุด้วยตัวอักษร W (แทนคำว่า White = ขาว) ตามด้วยตัวเลขของปีที่ส่ง เช่น W1
คือ สัญญาณที่ขาวส่งไปหาเขียวเมื่อสิ้นปีที่ 1 ของขาว เป็นต้น
ส่วนสัญญาณจากเขียวจะขึ้นต้นด้วยตัวอักษร G (แทนคำว่า Green = เขียว) ตามด้วยปีที่ส่งเช่นเดียวกัน เช่น G3
คือ สัญญาณที่เขียวส่งไปหาขาวเมื่อสิ้นปีที่ 3 ของเขียว เป็นต้น
ภาพที่ 4 (ซ้าย) แสดงสัญญาณที่ขาวส่งไปหาเขียว
จะเห็นว่าเขียวจะได้รับสัญญาณ W1 ตอนที่เดินทางไปถึงจุดหมายปลายทางพอดี
นั่นคือ เมื่อเวลาของขาวผ่านไป 5 ปี ในขณะที่เวลาของเขียวผ่านไปเพียง 3 ปี
(ผู้อ่านอาจลองคำนวณเพื่อตรวจสอบดูเอง)
ส่วนสัญญาณที่เหลือในปีที่ 2 (W2) ถึงปีที่ 10 (W10) นั้น เขียวจะได้รับแบบถี่ยิบในช่วงขากลับ
โดยครั้งสุดท้ายได้รับในปีที่ 6 ของเขียว (เท่ากับปีที่ 10 ของขาว) ตอนพบกันอีกครั้งหนึ่งพอดี
เมื่อเขียวได้รับสัญญาณ W1 ถึง W10 จากขาว รวม 10 ครั้ง เขียวย่อมระบุได้ว่า ขาวแก่เพิ่มขึ้น 10 ปี
ในทำนองเดียวกัน หากพิจารณาภาพที่ 4(ขวา) ซึ่งแสดงสัญญาณที่เขียวส่งไปหาขาว
จะเห็นว่าขาวได้รับสัญญาณจากเขียวทั้งสิ้น 6 ครั้ง ดังนั้นขาวย่อมสรุปจากหลักฐานนี้ว่าเขียวแก่เพิ่มขึ้นเพียง 6 ปี
นั่นคือ ตามทฤษฎีสัมพัทธภาพพิเศษ เขียวจึงแก่ช้ากว่าขาวเช่นกัน!
----------------------------------------------------------------------------------------
คำอธิบายนี้ เป็นการพูดด้านเดียว คือฝ่ายนายเขียว เดินทาง และใช้เวลาน้อยลง
ไม่มีการพูดถึง เวลาของนายขาวเลย
เป็นการตัดเหตการณ์เหลือข้างเดียว จึง ไม่เป็น Paradox
อ่านจบ ถ้าเรายัง งงๆ
ก็จะเข้าใจไปว่า คำอธิบายสมบูรณ์แล้ว
สรุปว่า ผู้เดินทางมีเวลาลดลงจริง ซะงั้น
ที่เรียกว่า เป็นการอธิบายแบบปักธงไว้ก่อน
ก็เพราะ ผู้อธิบาย มีความเชื่อว่า นายเขียวเป็นผู้เดินทางไป เปลี่ยนเฟรม และกลับ
การเชื่อเช่นนี้ เพราะผู้อธิบายเคยชินกับ สภาพนิ่งของโลก และจักรวาล
จึงเห็นว่า นายเขียวเดินทางไปกับยานและมีความเร็ว (แต่นายขาวไม่มีความเร็ว)
เป็นผลให้ เวลาของนายเขียวช้าลง
(และลืมมองตามโจทย์Paradox ว่านายเขียวเห็นนายขาวมีความเร็วด้วย)
โดยสรุป คำอธิบาย กลับกลายเป้นการอธิบายการเคลื่อนที่สัมบูรณ์
โดยมีโลก เป็นจุดอ้างอิงสัมบูรณ์
ซึ่ง หากผลของเวลายืดช้าลง เป็นฝ่ายนายเขียวจริง
ก็เท่ากับว่า ต้องพิจารณาเรื่อง จุดอ้างอิงสัมบูรณ์แล้ว