อวกาศลวงตาเราได้
กฏสัมพันธ์ไม่อาจใช้ได้กับทุกกรอบอ้างอิง
จากทฤษฎีสัมพัทธภาพของไอน์สไตน์คงจะพอรู้ว่า มีปริศนาน่าฉงนข้อหนึ่งซึ่งทำให้คนที่เริ่มเรียนรู้ทฤษฎีนี้ใหม่ๆ รู้สึกสับสน และทำให้คนที่ไม่เชื่อถือทฤษฎีนี้ใช้เป็นเหตุผลในการโจมตีว่า ทฤษฎีสัมพัทธภาพนั้นไม่น่าจะถูกต้อง 100% เพราะว่าคำอธิบายบางอย่างฟังแล้วขัดแย้งกันเอง ตัวปริศนาดังกล่าวมีเนื้อหาในทำนองนี้ครับ
ประเด็นเหตุการณ์ปริศนา – ที่มาของ ‘ปฏิทรรศน์ฝาแฝด’
สมมติว่ามีฝาแฝด 2 คน คือ ขาว และเขียว โดยทั้งสองคนนี้สนใจเรื่องราวเกี่ยวกับอวกาศ และเมื่อโตขึ้นก็ได้ทำงานในองค์การอวกาศทั้งคู่ โดยขาวเฝ้าประจำอยู่ที่ถานีอวกาศบนโลก (จำง่ายๆ แบบเกือบคล้องจองว่า ‘ขาวเฝ้าบ้าน’) ส่วนเขียวนั้นโชคดีมีโอกาสเดินทางไปในอวกาศด้วยยานอวกาศความเร็วสูง เพื่อสำรวจดาวฤกษ์ที่อยู่ห่างออกไปหลายปีแสง (จำง่ายๆ แบบคล้องจองว่า ‘เขียวท่องเที่ยวไป’) จากนั้นก็กลับมายังโลก
หนังสือหรือบทความเกี่ยวกับทฤษฎีสัมพัทธภาพมักจะอธิบายเหตุการณ์นี้สั้นๆ โดยสรุปว่า “เนื่องจากเขียวเดินทางออกจากโลกไปด้วยความเร็วสูง ทำให้นาฬิกาของเขียวเดินช้าลง (นั่นคือ เขียวแก่ช้ากว่าขาว) ตามหลักการยืดออกของเวลา (time dilation) ดังนั้น เมื่อทั้งคู่พบกันอีกครั้งก็จะพบว่า เขียวมีอายุน้อยกว่าขาว”
คำอธิบายในลักษณะนี้เองที่ทำให้คนที่คิดลึก (ไปอีก 1 ขั้น) แย้งว่า “อ้าว! ก็ทฤษฎีสัมพัทธภาพบอกว่า ความเร็วเป็นสัมพัทธ์ไงละ ดังนั้น หากคิดจากมุมของของเขียว (คนที่ ‘ท่องเที่ยวไป’) ดูบ้าง เขียวก็อาจจะพูดได้ว่า ตัวเขียวเองต่างหากที่อยู่นิ่งๆ ในยานอวกาศ ส่วนขาว (และโลกทั้งใบ!) เคลื่อนที่จากไปในช่วงแรก และเคลื่อนที่กลับเข้ามาหาเขาในช่วงหลัง”
ดังนั้น .. อะแฮ่ม! … เมื่อเขียวเห็นขาวเคลื่อนที่อยู่ฝ่ายเดียว เขียวก็ย่อมจะสรุปได้ว่า เวลาของขาวต้องเดินช้ากว่าของตัวเขียวเอง (นั่นคือ ขาวแก่ช้ากว่า) แสดงว่า เมื่อทั้งคู่พบกันอีกครั้ง ขาวต่างหากที่น่าจะเป็นคนที่มีอายุน้อยกว่า – ตรงกันข้ามกับข้อสรุปจากมุมมองของขาวที่เฝ้ารออยู่บนโลกโดยสิ้นเชิง
โดยสรุป เหตุผลสั้นๆ ในการโต้แย้งก็คือ
- ขาว (คนที่เฝ้าบนโลก) เห็นเขียวเคลื่อนที่ จึงบอกว่า เขียวแก่ช้ากว่าตนเอง
- เขียว (คนที่ท่องเที่ยวไป) เห็นขาวเคลื่อนที่ จึงบอกว่า ขาวแก่ช้ากว่าตนเอง
เมื่อทั้งขาวและเขียวสรุปออกมาตรงกันข้ามกันอย่างนี้ คนที่คิดว่าจับผิดทฤษฎีของไอน์สไตน์ได้ก็เลยฟันธงว่า เนื่องจากทฤษฎีสัมพัทธภาพให้ข้อสรุปที่ขัดแย้งกันเอง ดังนั้นจึงเชื่อถือไม่ได้ – นี่คือที่มาของ ปฏิทรรศน์ฝาแฝด (Twin Paradox) ซึ่งเรียกอีกชื่อหนึ่งว่า ปฏิทรรศน์นาฬิกา (Clock Paradox)
คำว่า ปฏิทรรศน์ (paradox) หมายถึง ข้อความหรือคำอธิบายที่มีเหตุผลรองรับอย่างดี แต่ฟังแล้วขัดแย้งกับความเชื่อที่ถือกันโดยทั่วไปว่าถูกต้อง (ปฏิ- = ตรงกันข้าม + ทรรศนะ = ความคิดเห็น หรือสิ่งที่เห็น) แล้วอย่างนี้ เราจะช่วย “เถียง” แทนไอน์สไตน์ได้ยังไงบ้าง?
ชำแหละปฏิทรรศน์ฝาแฝด
การที่ประเด็นนี้กลายเป็นปัญหาขึ้นมาเนื่องจากคำอธิบายที่ว่า
“เขียวไปกับยานอวกาศความเร็วสูงทำให้แก่ช้ากว่าขาว” นั้นสั้นและง่ายเกินไป ดังนั้น เราจำเป็นต้องเจาะลึกและวิเคราะห์ปัญหานี้ให้ละเอียดขึ้นตลอดเส้นทางการเดินทางตั้งแต่ต้นจนจบ เพื่อให้เข้าใจการประยุกต์ทฤษฎีสัมพัทธภาพอย่างถูกต้อง
เพื่อให้เหตุการณ์ชัดเจนยิ่งขึ้น จะขอสมมติว่า เขียวเดินทางไปเยือนดาวฤกษ์เป้าหมายซึ่งอยู่ห่างจากโลกเป็นระยะทาง L = 4 ปีแสง และเมื่อเขียวไปถึงที่หมายแล้วก็วกยานกลับมายังโลก โดยไม่ได้หยุดแวะพักตลอดการเดินทาง (เพื่อให้การคำนวณและการอธิบายกระชับขึ้น แต่ไม่สูญเสียสาระสำคัญ)
การอธิบายปฏิทรรศน์ฝาแฝดอาจทำได้อย่างน้อยวิธีหลักๆ ได้แก่
ใช้ทฤษฎีสัมพัทธภาพทั่วไป (General Relativity)
ใช้ทฤษฎีสัมพัทธภาพพิเศษ (Special Relativity)
แต่ไม่ว่าใช้วิธีการใดก็ตาม คำอธิบายจะเข้าใจได้ง่ายขึ้น หากเราใช้แผนภาพกาลอวกาศ (spacetime diagram) มาช่วยให้เห็นเส้นทางการเคลื่อนที่ของขาวและเขียวไปในอวกาศ (space) และเวลา (time) เปรียบเทียบกัน ดังนั้น จึงน่าจะมาทบทวนแผนภาพดังกล่าวก่อนดังนี้
เพื่อให้เนื้อหากระชับ จะขอถือว่า ผู้อ่านเข้าใจพื้นฐานของแผนภาพอวกาศดีพอสมควรแล้ว ดังนั้น ผมจะขอเริ่มจากการอธิบายด้วยทฤษฎีสัมพัทธภาพทั่วไปก่อน เพราะในความเห็นของผม เข้าใจง่ายกว่าและฟังเป็นธรรมชาติมากกว่า หลังจากนั้นก็ลองพิจารณาคำอธิบายโดยใช้ทฤษฎีสัมพัทธภาพพิเศษแบบละเอียดพอสมควร และมีการคำนวณประกอบเล็กน้อย
วิธีที่ 1 : อธิบายด้วย ‘ทฤษฎีสัมพัทธภาพทั่วไป’
ลองจินตนาการเหตุการณ์นี้ให้ละเอียดขึ้นอีกนิดดังนี้ เดิมทีขาวกับเขียวอยู่บนโลก จากนั้นเขียวก็ขึ้นยานอวกาศจากไป โดยยานอวกาศจะเร่งอัตราเร็วเพื่อให้หลุดจากแรงโน้มถ่วงของโลก เมื่อเวลาผ่านไปสักพักหนึ่ง ยานจะเคลื่อนที่ด้วยความเร็วค่อนข้างคงที่ (แต่ก็เร็วมากเกือบเท่ากับอัตราเร็วแสง) เมื่อใกล้ถึงที่หมาย เขียวจะหน่วงยานให้ช้าลง แล้ววกกลับทิศทาง ณ บริเวณที่หมาย จากนั้นก็เร่งเครื่องหนีจากที่หมาย แล้วเดินทางด้วยอัตราเร็วค่อนข้างคงที่ตรงกลับมายังโลก โดยเมื่อใกล้ถึงโลก เขียวก็ต้องลดอัตราเร็วของยานลงเพื่อลงจอดที่สถานีและพบขาวในที่สุด
เหตุการณ์ทั้งหมดนี้แสดงด้วยภาพที่ 3 ซึ่งเป็นแผนภาพกาลอวกาศในมุมมองของขาวซึ่งอยู่บนโลก
เนื่องจากเขียวต้องมีความเร่ง (หรือความหน่วง) ถึง 4 ครั้ง ได้แก่
หนึ่ง - เร่งตอนช่วงเริ่มออกเดินทาง
สอง - หน่วงตอนเข้าใกล้ที่หมาย
สาม - เร่งหนีออกจากที่หมาย และ
สี่ - หน่วงเมื่อเข้าใกล้โลกตอนขากลับ
ดังนั้น เวลาของเขียวจะเดินช้าลง ตามทฤษฎีสัมพัทธภาพทั่วไปซึ่งกล่าวว่า ความเร่ง (หรือความหน่วง) สมมูลกับความโน้มถ่วง โดยทั้งความเร่งและความโน้มถ่วงสามารถทำให้นาฬิกาเดินช้าลงได้เช่นกัน ดังนั้น หากเวลาของขาว (ซึ่งเฝ้าอยู่บนโลก) ผ่านไประยะหนึ่ง ซึ่งสมมติว่าเป็น 10 ปี ก็จะพบว่าเวลาของเขียวจะผ่านไปไม่ถึง 10 ปี (ตัวเลข 10 ปีนี้ ยกขึ้นมาเพื่อให้สามารถเปรียบเทียบกับผลการคำนวณด้วยทฤษฎีสัมพัทธภาพพิเศษ ซึ่งจะได้กล่าวถึงในหัวข้อต่อไป)
ดังนั้น ตามทฤษฎีสัมพัทธภาพทั่วไป เขียวจึงแก่ช้ากว่าขาวอย่างแน่นอน!
วิธีที่ 2 : อธิบายด้วย ‘ทฤษฎีสัมพัทธภาพพิเศษ’
นักฟิสิกส์ชั้นนำจำนวนหนึ่งเชื่อว่า เราสามารถใช้แค่ทฤษฎีสัมพัทธภาพพิเศษเพื่ออธิบายปฏิทรรศน์ฝาแฝดก็เพียงพอแล้ว!
อย่างไรก็ตามต้องตระหนักไว้ว่า เหตุการณ์ต่างๆ ที่เกิดขึ้นกับขาวและเขียวนั้นต่างกัน เนื่องจาก ขาวอยู่ในกรอบเฉื่อยกรอบเดียวตลอดเวลา โดยอาจสมมติว่าโลกเป็นจุดนิ่งๆ ในอวกาศ และไม่มีแรงโน้มถ่วง (หรือถ้ายังไม่ชอบการสมมติแบบนี้ ก็อาจคิดว่า ‘โลก’ เป็นสถานีอวกาศที่ลอยอยู่นิ่งๆ ก็ได้)
ส่วนเขียวซึ่งเดินทางไปกับยานอวกาศนั้นได้เปลี่ยนกรอบอ้างอิงอย่างน้อย 1 ครั้ง ในช่วงหักยานวกกลับมายังโลก นั่นคือ ในช่วงขาไป เขียวไปกับยาน A ที่เคลื่อนที่หนีออกจากโลกด้วยอัตราเร็วคงที่ พอไปถึงที่หมายก็มียาน B ซึ่งเคลื่อนที่เข้าหาโลกด้วยอัตราเร็วเท่าๆ กัน (แต่ทิศทางกลับกับยาน B) มาแวะรับเขียวกลับพอดี หากจินตนาการตามนี้เขียวจะอยู่ในกรอบของยาน A ตอนขาไป และอยู่ในกรอบ (อีกกรอบหนึ่ง) ของยาน B ตอนขากลับ ประเด็นเรื่องการเปลี่ยนกรอบอ้างอิงนี้สำคัญ เพราะเป็นเหตุผลในการอธิบายปริทรรศน์ฝาแฝดโดยใช้ทฤษฎีสัมพัทธภาพพิเศษนั่นเอง
ในเบื้องต้นนี้ สมมติให้ ระยะทางจากดวงดาวที่หมายเป็น L=4 ปีแสง (เช่นเดิม) และอัตราเร็วของยานในช่วงเดินทาง v = (4/5)c = 0.8 เท่าของอัตราเร็วของแสง
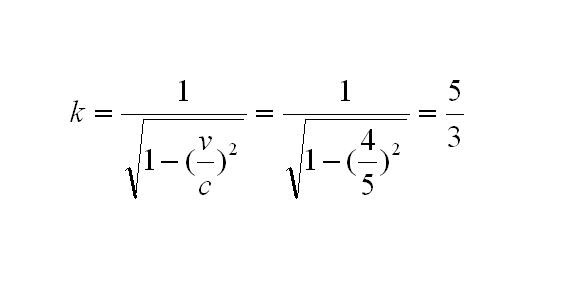
นั่นคือ แฟกเตอร์การยืด (stretch factor) k ในสูตรการแปลงแบบลอเรนซ์มีค่าเท่ากับ 5/3 (แสดงสูตรการแปลงดังภาพที่ 3) เมื่อทราบตัวเลขที่จำเป็นในการคำนวณแล้ว คราวนี้ลองมาดูเหตุการณ์ในมุมมองของแต่ละคนดูบ้าง
มุมมองของขาว (‘เฝ้าบ้าน’)
มุมมองของเขียว (‘ท่องเที่ยวไป’)
ขาวจะบอกว่า เขียวต้องใช้เวลาเดินทางไปถึงที่หมาย
Dt1= L/v = (4 ปีแสง)/(0.8 c) = 5 ปี
และใช้เวลาเดินทางกลับเท่าๆ กัน นั่นคือ
Dt2 = 5 ปี
รวมเวลาที่ขาวต้องรอเขียวกลับมายังโลก
Dt1 + Dt2= 5 ปี + 5 ปี = 10 ปี
นั่นคือ ขาวต้องรอถึง 10 ปี กว่าจะพบกับเขียว เขียวบอกว่าระยะทางขาไปนั้น จะหดสั้นเหลือแค่
L' = L/k = (4 ปีแสง)/(5/3) = 12/5 ปีแสง = 2.4 ปีแสง
และเนื่องจากเขียวเดินทางด้วยอัตราเร็ว v=0.8c
ดังนั้น เขาจะถึงที่หมายในเวลา
Dt'1 = L'/v = (2.4 ปีแสง)/(0.8 c) = 3 ปี
โดยขากลับ (แม้จะอยู่ในอีกกรอบหนึ่ง) ก็จะใช้เวลาเท่ากัน คือ
Dt'2= 3 ปี
รวมเวลาในการเดินทางของเขียวทั้งหมด
Dt'1 + Dt'2 3 ปี + 3 ปี = 6 ปี
นั่นคือ เวลาของเขียวผ่านไปเพียง 6 ปี ก็พบกับขาวแล้ว
เพื่อให้เห็นเหตุการณ์ชัดเจนขึ้น สมมติว่า แต่ละคนส่งสัญญานคลื่นแม่เหล็กไฟฟ้า (เช่น สัญญาณวิทยุ) กลับไปหาอีกฝ่ายปีละ 1 ครั้ง คำถามก็คือ แต่ละฝ่ายจะได้รับสัญญาณกี่ครั้ง? เมื่อไรบ้าง?
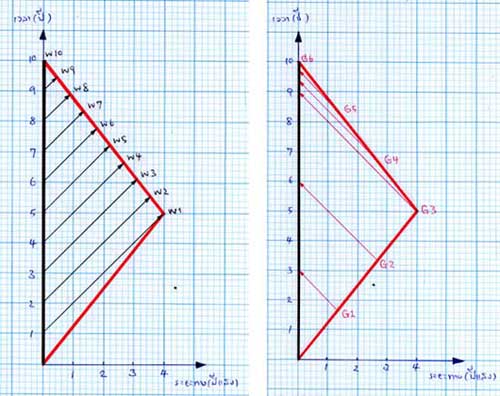
ภาพที่ 4 เป็นแผนภาพกาลอวกาศจากมุมมองของขาวซึ่งน่าจะช่วยให้เห็นเหตุการณ์นี้ชัดเจนขึ้น โดยสัญญาณที่ขาวส่งไประบุด้วยตัวอักษร W (แทนคำว่า White = ขาว) ตามด้วยตัวเลขของปีที่ส่ง เช่น W1 คือ สัญญาณที่ขาวส่งไปหาเขียวเมื่อสิ้นปีที่ 1 ของขาว เป็นต้น ส่วนสัญญาณจากเขียวจะขึ้นต้นด้วยตัวอักษร G (แทนคำว่า Green = เขียว) ตามด้วยปีที่ส่งเช่นเดียวกัน เช่น G3 คือ สัญญาณที่เขียวส่งไปหาขาวเมื่อสิ้นปีที่ 3 ของเขียว เป็นต้น
ภาพที่ 4 (ซ้าย) แสดงสัญญาณที่ขาวส่งไปหาเขียว จะเห็นว่าเขียวจะได้รับสัญญาณ W1 ตอนที่เดินทางไปถึงจุดหมายปลายทางพอดี นั่นคือ เมื่อเวลาของขาวผ่านไป 5 ปี ในขณะที่เวลาของเขียวผ่านไปเพียง 3 ปี (ผู้อ่านอาจลองคำนวณเพื่อตรวจสอบดูเอง) ส่วนสัญญาณที่เหลือในปีที่ 2 (W2) ถึงปีที่ 10 (W10) นั้น เขียวจะได้รับแบบถี่ยิบในช่วงขากลับ โดยครั้งสุดท้ายได้รับในปีที่ 6 ของเขียว (เท่ากับปีที่ 10 ของขาว) ตอนพบกันอีกครั้งหนึ่งพอดี เมื่อเขียวได้รับสัญญาณ W1 ถึง W10 จากขาว รวม 10 ครั้ง เขียวย่อมระบุได้ว่า ขาวแก่เพิ่มขึ้น 10 ปี
ในทำนองเดียวกัน หากพิจารณาภาพที่ 4(ขวา) ซึ่งแสดงสัญญาณที่เขียวส่งไปหาขาว จะเห็นว่าขาวได้รับสัญญาณจากเขียวทั้งสิ้น 6 ครั้ง ดังนั้นขาวย่อมสรุปจากหลักฐานนี้ว่าเขียวแก่เพิ่มขึ้นเพียง 6 ปี
นั่นคือ ตามทฤษฎีสัมพัทธภาพพิเศษ เขียวจึงแก่ช้ากว่าขาวเช่นกัน!
ขอบคุณข้อมูลจาก
http://www.manager.co.th/Science/ViewNews.aspx?NewsID=9480000121618
(เอาบทความมาฝาก) ปฏิทรรศน์ฝาแฝด ทำไมถึงไม่เป็นจริง...
กฏสัมพันธ์ไม่อาจใช้ได้กับทุกกรอบอ้างอิง
จากทฤษฎีสัมพัทธภาพของไอน์สไตน์คงจะพอรู้ว่า มีปริศนาน่าฉงนข้อหนึ่งซึ่งทำให้คนที่เริ่มเรียนรู้ทฤษฎีนี้ใหม่ๆ รู้สึกสับสน และทำให้คนที่ไม่เชื่อถือทฤษฎีนี้ใช้เป็นเหตุผลในการโจมตีว่า ทฤษฎีสัมพัทธภาพนั้นไม่น่าจะถูกต้อง 100% เพราะว่าคำอธิบายบางอย่างฟังแล้วขัดแย้งกันเอง ตัวปริศนาดังกล่าวมีเนื้อหาในทำนองนี้ครับ
ประเด็นเหตุการณ์ปริศนา – ที่มาของ ‘ปฏิทรรศน์ฝาแฝด’
สมมติว่ามีฝาแฝด 2 คน คือ ขาว และเขียว โดยทั้งสองคนนี้สนใจเรื่องราวเกี่ยวกับอวกาศ และเมื่อโตขึ้นก็ได้ทำงานในองค์การอวกาศทั้งคู่ โดยขาวเฝ้าประจำอยู่ที่ถานีอวกาศบนโลก (จำง่ายๆ แบบเกือบคล้องจองว่า ‘ขาวเฝ้าบ้าน’) ส่วนเขียวนั้นโชคดีมีโอกาสเดินทางไปในอวกาศด้วยยานอวกาศความเร็วสูง เพื่อสำรวจดาวฤกษ์ที่อยู่ห่างออกไปหลายปีแสง (จำง่ายๆ แบบคล้องจองว่า ‘เขียวท่องเที่ยวไป’) จากนั้นก็กลับมายังโลก
หนังสือหรือบทความเกี่ยวกับทฤษฎีสัมพัทธภาพมักจะอธิบายเหตุการณ์นี้สั้นๆ โดยสรุปว่า “เนื่องจากเขียวเดินทางออกจากโลกไปด้วยความเร็วสูง ทำให้นาฬิกาของเขียวเดินช้าลง (นั่นคือ เขียวแก่ช้ากว่าขาว) ตามหลักการยืดออกของเวลา (time dilation) ดังนั้น เมื่อทั้งคู่พบกันอีกครั้งก็จะพบว่า เขียวมีอายุน้อยกว่าขาว”
คำอธิบายในลักษณะนี้เองที่ทำให้คนที่คิดลึก (ไปอีก 1 ขั้น) แย้งว่า “อ้าว! ก็ทฤษฎีสัมพัทธภาพบอกว่า ความเร็วเป็นสัมพัทธ์ไงละ ดังนั้น หากคิดจากมุมของของเขียว (คนที่ ‘ท่องเที่ยวไป’) ดูบ้าง เขียวก็อาจจะพูดได้ว่า ตัวเขียวเองต่างหากที่อยู่นิ่งๆ ในยานอวกาศ ส่วนขาว (และโลกทั้งใบ!) เคลื่อนที่จากไปในช่วงแรก และเคลื่อนที่กลับเข้ามาหาเขาในช่วงหลัง”
ดังนั้น .. อะแฮ่ม! … เมื่อเขียวเห็นขาวเคลื่อนที่อยู่ฝ่ายเดียว เขียวก็ย่อมจะสรุปได้ว่า เวลาของขาวต้องเดินช้ากว่าของตัวเขียวเอง (นั่นคือ ขาวแก่ช้ากว่า) แสดงว่า เมื่อทั้งคู่พบกันอีกครั้ง ขาวต่างหากที่น่าจะเป็นคนที่มีอายุน้อยกว่า – ตรงกันข้ามกับข้อสรุปจากมุมมองของขาวที่เฝ้ารออยู่บนโลกโดยสิ้นเชิง
โดยสรุป เหตุผลสั้นๆ ในการโต้แย้งก็คือ
- ขาว (คนที่เฝ้าบนโลก) เห็นเขียวเคลื่อนที่ จึงบอกว่า เขียวแก่ช้ากว่าตนเอง
- เขียว (คนที่ท่องเที่ยวไป) เห็นขาวเคลื่อนที่ จึงบอกว่า ขาวแก่ช้ากว่าตนเอง
เมื่อทั้งขาวและเขียวสรุปออกมาตรงกันข้ามกันอย่างนี้ คนที่คิดว่าจับผิดทฤษฎีของไอน์สไตน์ได้ก็เลยฟันธงว่า เนื่องจากทฤษฎีสัมพัทธภาพให้ข้อสรุปที่ขัดแย้งกันเอง ดังนั้นจึงเชื่อถือไม่ได้ – นี่คือที่มาของ ปฏิทรรศน์ฝาแฝด (Twin Paradox) ซึ่งเรียกอีกชื่อหนึ่งว่า ปฏิทรรศน์นาฬิกา (Clock Paradox)
คำว่า ปฏิทรรศน์ (paradox) หมายถึง ข้อความหรือคำอธิบายที่มีเหตุผลรองรับอย่างดี แต่ฟังแล้วขัดแย้งกับความเชื่อที่ถือกันโดยทั่วไปว่าถูกต้อง (ปฏิ- = ตรงกันข้าม + ทรรศนะ = ความคิดเห็น หรือสิ่งที่เห็น) แล้วอย่างนี้ เราจะช่วย “เถียง” แทนไอน์สไตน์ได้ยังไงบ้าง?
ชำแหละปฏิทรรศน์ฝาแฝด
การที่ประเด็นนี้กลายเป็นปัญหาขึ้นมาเนื่องจากคำอธิบายที่ว่า
“เขียวไปกับยานอวกาศความเร็วสูงทำให้แก่ช้ากว่าขาว” นั้นสั้นและง่ายเกินไป ดังนั้น เราจำเป็นต้องเจาะลึกและวิเคราะห์ปัญหานี้ให้ละเอียดขึ้นตลอดเส้นทางการเดินทางตั้งแต่ต้นจนจบ เพื่อให้เข้าใจการประยุกต์ทฤษฎีสัมพัทธภาพอย่างถูกต้อง
เพื่อให้เหตุการณ์ชัดเจนยิ่งขึ้น จะขอสมมติว่า เขียวเดินทางไปเยือนดาวฤกษ์เป้าหมายซึ่งอยู่ห่างจากโลกเป็นระยะทาง L = 4 ปีแสง และเมื่อเขียวไปถึงที่หมายแล้วก็วกยานกลับมายังโลก โดยไม่ได้หยุดแวะพักตลอดการเดินทาง (เพื่อให้การคำนวณและการอธิบายกระชับขึ้น แต่ไม่สูญเสียสาระสำคัญ)
การอธิบายปฏิทรรศน์ฝาแฝดอาจทำได้อย่างน้อยวิธีหลักๆ ได้แก่
ใช้ทฤษฎีสัมพัทธภาพทั่วไป (General Relativity)
ใช้ทฤษฎีสัมพัทธภาพพิเศษ (Special Relativity)
แต่ไม่ว่าใช้วิธีการใดก็ตาม คำอธิบายจะเข้าใจได้ง่ายขึ้น หากเราใช้แผนภาพกาลอวกาศ (spacetime diagram) มาช่วยให้เห็นเส้นทางการเคลื่อนที่ของขาวและเขียวไปในอวกาศ (space) และเวลา (time) เปรียบเทียบกัน ดังนั้น จึงน่าจะมาทบทวนแผนภาพดังกล่าวก่อนดังนี้
เพื่อให้เนื้อหากระชับ จะขอถือว่า ผู้อ่านเข้าใจพื้นฐานของแผนภาพอวกาศดีพอสมควรแล้ว ดังนั้น ผมจะขอเริ่มจากการอธิบายด้วยทฤษฎีสัมพัทธภาพทั่วไปก่อน เพราะในความเห็นของผม เข้าใจง่ายกว่าและฟังเป็นธรรมชาติมากกว่า หลังจากนั้นก็ลองพิจารณาคำอธิบายโดยใช้ทฤษฎีสัมพัทธภาพพิเศษแบบละเอียดพอสมควร และมีการคำนวณประกอบเล็กน้อย
วิธีที่ 1 : อธิบายด้วย ‘ทฤษฎีสัมพัทธภาพทั่วไป’
ลองจินตนาการเหตุการณ์นี้ให้ละเอียดขึ้นอีกนิดดังนี้ เดิมทีขาวกับเขียวอยู่บนโลก จากนั้นเขียวก็ขึ้นยานอวกาศจากไป โดยยานอวกาศจะเร่งอัตราเร็วเพื่อให้หลุดจากแรงโน้มถ่วงของโลก เมื่อเวลาผ่านไปสักพักหนึ่ง ยานจะเคลื่อนที่ด้วยความเร็วค่อนข้างคงที่ (แต่ก็เร็วมากเกือบเท่ากับอัตราเร็วแสง) เมื่อใกล้ถึงที่หมาย เขียวจะหน่วงยานให้ช้าลง แล้ววกกลับทิศทาง ณ บริเวณที่หมาย จากนั้นก็เร่งเครื่องหนีจากที่หมาย แล้วเดินทางด้วยอัตราเร็วค่อนข้างคงที่ตรงกลับมายังโลก โดยเมื่อใกล้ถึงโลก เขียวก็ต้องลดอัตราเร็วของยานลงเพื่อลงจอดที่สถานีและพบขาวในที่สุด
เหตุการณ์ทั้งหมดนี้แสดงด้วยภาพที่ 3 ซึ่งเป็นแผนภาพกาลอวกาศในมุมมองของขาวซึ่งอยู่บนโลก
เนื่องจากเขียวต้องมีความเร่ง (หรือความหน่วง) ถึง 4 ครั้ง ได้แก่
หนึ่ง - เร่งตอนช่วงเริ่มออกเดินทาง
สอง - หน่วงตอนเข้าใกล้ที่หมาย
สาม - เร่งหนีออกจากที่หมาย และ
สี่ - หน่วงเมื่อเข้าใกล้โลกตอนขากลับ
ดังนั้น เวลาของเขียวจะเดินช้าลง ตามทฤษฎีสัมพัทธภาพทั่วไปซึ่งกล่าวว่า ความเร่ง (หรือความหน่วง) สมมูลกับความโน้มถ่วง โดยทั้งความเร่งและความโน้มถ่วงสามารถทำให้นาฬิกาเดินช้าลงได้เช่นกัน ดังนั้น หากเวลาของขาว (ซึ่งเฝ้าอยู่บนโลก) ผ่านไประยะหนึ่ง ซึ่งสมมติว่าเป็น 10 ปี ก็จะพบว่าเวลาของเขียวจะผ่านไปไม่ถึง 10 ปี (ตัวเลข 10 ปีนี้ ยกขึ้นมาเพื่อให้สามารถเปรียบเทียบกับผลการคำนวณด้วยทฤษฎีสัมพัทธภาพพิเศษ ซึ่งจะได้กล่าวถึงในหัวข้อต่อไป)
ดังนั้น ตามทฤษฎีสัมพัทธภาพทั่วไป เขียวจึงแก่ช้ากว่าขาวอย่างแน่นอน!
วิธีที่ 2 : อธิบายด้วย ‘ทฤษฎีสัมพัทธภาพพิเศษ’
นักฟิสิกส์ชั้นนำจำนวนหนึ่งเชื่อว่า เราสามารถใช้แค่ทฤษฎีสัมพัทธภาพพิเศษเพื่ออธิบายปฏิทรรศน์ฝาแฝดก็เพียงพอแล้ว!
อย่างไรก็ตามต้องตระหนักไว้ว่า เหตุการณ์ต่างๆ ที่เกิดขึ้นกับขาวและเขียวนั้นต่างกัน เนื่องจาก ขาวอยู่ในกรอบเฉื่อยกรอบเดียวตลอดเวลา โดยอาจสมมติว่าโลกเป็นจุดนิ่งๆ ในอวกาศ และไม่มีแรงโน้มถ่วง (หรือถ้ายังไม่ชอบการสมมติแบบนี้ ก็อาจคิดว่า ‘โลก’ เป็นสถานีอวกาศที่ลอยอยู่นิ่งๆ ก็ได้)
ส่วนเขียวซึ่งเดินทางไปกับยานอวกาศนั้นได้เปลี่ยนกรอบอ้างอิงอย่างน้อย 1 ครั้ง ในช่วงหักยานวกกลับมายังโลก นั่นคือ ในช่วงขาไป เขียวไปกับยาน A ที่เคลื่อนที่หนีออกจากโลกด้วยอัตราเร็วคงที่ พอไปถึงที่หมายก็มียาน B ซึ่งเคลื่อนที่เข้าหาโลกด้วยอัตราเร็วเท่าๆ กัน (แต่ทิศทางกลับกับยาน B) มาแวะรับเขียวกลับพอดี หากจินตนาการตามนี้เขียวจะอยู่ในกรอบของยาน A ตอนขาไป และอยู่ในกรอบ (อีกกรอบหนึ่ง) ของยาน B ตอนขากลับ ประเด็นเรื่องการเปลี่ยนกรอบอ้างอิงนี้สำคัญ เพราะเป็นเหตุผลในการอธิบายปริทรรศน์ฝาแฝดโดยใช้ทฤษฎีสัมพัทธภาพพิเศษนั่นเอง
ในเบื้องต้นนี้ สมมติให้ ระยะทางจากดวงดาวที่หมายเป็น L=4 ปีแสง (เช่นเดิม) และอัตราเร็วของยานในช่วงเดินทาง v = (4/5)c = 0.8 เท่าของอัตราเร็วของแสง
นั่นคือ แฟกเตอร์การยืด (stretch factor) k ในสูตรการแปลงแบบลอเรนซ์มีค่าเท่ากับ 5/3 (แสดงสูตรการแปลงดังภาพที่ 3) เมื่อทราบตัวเลขที่จำเป็นในการคำนวณแล้ว คราวนี้ลองมาดูเหตุการณ์ในมุมมองของแต่ละคนดูบ้าง
มุมมองของขาว (‘เฝ้าบ้าน’)
มุมมองของเขียว (‘ท่องเที่ยวไป’)
ขาวจะบอกว่า เขียวต้องใช้เวลาเดินทางไปถึงที่หมาย
Dt1= L/v = (4 ปีแสง)/(0.8 c) = 5 ปี
และใช้เวลาเดินทางกลับเท่าๆ กัน นั่นคือ
Dt2 = 5 ปี
รวมเวลาที่ขาวต้องรอเขียวกลับมายังโลก
Dt1 + Dt2= 5 ปี + 5 ปี = 10 ปี
นั่นคือ ขาวต้องรอถึง 10 ปี กว่าจะพบกับเขียว เขียวบอกว่าระยะทางขาไปนั้น จะหดสั้นเหลือแค่
L' = L/k = (4 ปีแสง)/(5/3) = 12/5 ปีแสง = 2.4 ปีแสง
และเนื่องจากเขียวเดินทางด้วยอัตราเร็ว v=0.8c
ดังนั้น เขาจะถึงที่หมายในเวลา
Dt'1 = L'/v = (2.4 ปีแสง)/(0.8 c) = 3 ปี
โดยขากลับ (แม้จะอยู่ในอีกกรอบหนึ่ง) ก็จะใช้เวลาเท่ากัน คือ
Dt'2= 3 ปี
รวมเวลาในการเดินทางของเขียวทั้งหมด
Dt'1 + Dt'2 3 ปี + 3 ปี = 6 ปี
นั่นคือ เวลาของเขียวผ่านไปเพียง 6 ปี ก็พบกับขาวแล้ว
เพื่อให้เห็นเหตุการณ์ชัดเจนขึ้น สมมติว่า แต่ละคนส่งสัญญานคลื่นแม่เหล็กไฟฟ้า (เช่น สัญญาณวิทยุ) กลับไปหาอีกฝ่ายปีละ 1 ครั้ง คำถามก็คือ แต่ละฝ่ายจะได้รับสัญญาณกี่ครั้ง? เมื่อไรบ้าง?
ภาพที่ 4 เป็นแผนภาพกาลอวกาศจากมุมมองของขาวซึ่งน่าจะช่วยให้เห็นเหตุการณ์นี้ชัดเจนขึ้น โดยสัญญาณที่ขาวส่งไประบุด้วยตัวอักษร W (แทนคำว่า White = ขาว) ตามด้วยตัวเลขของปีที่ส่ง เช่น W1 คือ สัญญาณที่ขาวส่งไปหาเขียวเมื่อสิ้นปีที่ 1 ของขาว เป็นต้น ส่วนสัญญาณจากเขียวจะขึ้นต้นด้วยตัวอักษร G (แทนคำว่า Green = เขียว) ตามด้วยปีที่ส่งเช่นเดียวกัน เช่น G3 คือ สัญญาณที่เขียวส่งไปหาขาวเมื่อสิ้นปีที่ 3 ของเขียว เป็นต้น
ภาพที่ 4 (ซ้าย) แสดงสัญญาณที่ขาวส่งไปหาเขียว จะเห็นว่าเขียวจะได้รับสัญญาณ W1 ตอนที่เดินทางไปถึงจุดหมายปลายทางพอดี นั่นคือ เมื่อเวลาของขาวผ่านไป 5 ปี ในขณะที่เวลาของเขียวผ่านไปเพียง 3 ปี (ผู้อ่านอาจลองคำนวณเพื่อตรวจสอบดูเอง) ส่วนสัญญาณที่เหลือในปีที่ 2 (W2) ถึงปีที่ 10 (W10) นั้น เขียวจะได้รับแบบถี่ยิบในช่วงขากลับ โดยครั้งสุดท้ายได้รับในปีที่ 6 ของเขียว (เท่ากับปีที่ 10 ของขาว) ตอนพบกันอีกครั้งหนึ่งพอดี เมื่อเขียวได้รับสัญญาณ W1 ถึง W10 จากขาว รวม 10 ครั้ง เขียวย่อมระบุได้ว่า ขาวแก่เพิ่มขึ้น 10 ปี
ในทำนองเดียวกัน หากพิจารณาภาพที่ 4(ขวา) ซึ่งแสดงสัญญาณที่เขียวส่งไปหาขาว จะเห็นว่าขาวได้รับสัญญาณจากเขียวทั้งสิ้น 6 ครั้ง ดังนั้นขาวย่อมสรุปจากหลักฐานนี้ว่าเขียวแก่เพิ่มขึ้นเพียง 6 ปี
นั่นคือ ตามทฤษฎีสัมพัทธภาพพิเศษ เขียวจึงแก่ช้ากว่าขาวเช่นกัน!
ขอบคุณข้อมูลจาก
http://www.manager.co.th/Science/ViewNews.aspx?NewsID=9480000121618