ลองดูเหตุการณ์สมมติสองเหตุการณ์
1. เพิ่ม 10% แล้วลด 10% จริงๆแล้วสุทธิคือ -1% ไม่ใช่เท่าเดิม : (100% + 10%) x (100% - 10%) = 100% - 1%
2. แบ่งเงินออกเป็นสองส่วนเท่าๆกัน ส่วนแรกได้กำไร 10% ส่วนที่สองขาดทุน 10% ผลคือเท่าทุน : 50% x (100% + 10%) + 50% x (100% - 10%) = 100% + 0%
เพราะอะไร : เหตุผลคือ ความมั่งคั่งของเรา มีลักษณะ geometric ในแนว longitude และมีลักษณะ arithmetric ในแนว cross section นั่นเอง
ผมชอบมอง return ใน scale log เพราะมันมีคุณสมบัติ additivity ในช่วงเวลาต่างๆกัน
สมมติว่าเรา ได้กำไร 25% และขาดทุน 20% สุทธิคือ 1.25 x .8 = 1 นั่นคือ เท่าทุน ซึ่ง (0.25+ -0.2) <> 0 นั่นคือ ตัว return ไม่มี additivity
แต่หากลองเปลี่ยนมุมมองใหม่เป็น log return : ln(1.25)+ln(0.8) จะได้ว่า log return ของมันมี additivity, เหตุผล :
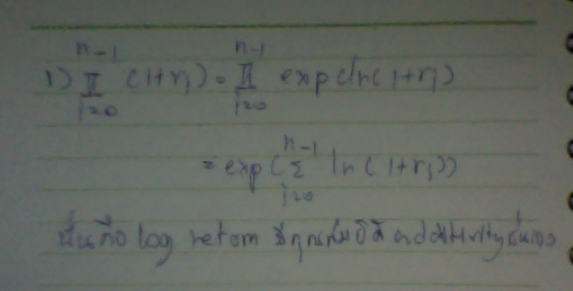
นอกจากจะมีคุณสมบัติ additivity แล้ว ยังมีสิ่งที่น่าสนใจอีกหลายประการ หนึ่งในนั้นก็คือ ในช่วงระยะสั้นๆ ที่ return ขนาดต่ำๆ ค่าของ log return จะใกล้เคียงกับค่าของ return
เหตุผล :


การที่มันเน้นย้ำฝั่งขาดทุน และลดทอนฝั่งกำไร ช่วยให้เรามองเห็นภาพพจน์ได้ชัดเจนขึ้น และช่วยรักษาคุณสมบัติ additivity ไว้ได้ และที่ขนาดน้อยๆ ค่าของมันค่อนข้างใกล้เคียงกับค่า return ปรกติ
อีกหนึ่งเหตุผลที่น่าสนใจ นั่นคือ สมมติฐานของโลกการเงินมักอยู่บน log normality จึงเป็นการสมเหตุผลผลมากกว่าหากเราจะใช้ log return
ทำไมนะหรือ ลองเปรียบเทียบ normality กับ log normality หากเรายอมรับ normality ก็หมายความว่า เรายอมรับว่าราคาหุ้นอาจขึ้นหรือตาม return แบบสุ่ม เช่นเดือนนี้อาจขึ้น 100% พรุ่งนี้ลง 120% ก็ได้
ในแต่ความเป็นจริง ไม่ได้ เพราะเราไม่ยอมรับราคาหุ้นที่ติดลบ หรือแม้กระทั้งเป็น 0
การที่เรายอมรับ log normality นั่นก็หมายถืง เรายอมรับราคาหุ้นที่เป็นบวกเท่านั้น เพราะ Exp(ln(1+R)) มีค่าเป็นบวกเสมอ นั่นคือ R > - 100% อยู่บนสมมติฐานที่ว่าราคาหุ้น จะไม่ถูกซื้อขายที่ 0 บาทหรือติดลบ
ทั้งนี้ทั้งนั้น ผมไม่ได้มาโปรโมทการใช้ scale log หรืออย่างไร แต่เพียงมาเสนอมุมมองดูครับ อาจเป็นประโยชน์ต่อเพื่อนๆนักลงทุน
สุดท้ายนี้ สวัสดีปีใหม่ ขอให้มีแต่สิ่งที่ดีงามเข้ามาในชีวิต คิดอะไรประสบสมหวังทุกประการครับผม

log return อีกมุมมองที่ดีไม่แพ้ return
1. เพิ่ม 10% แล้วลด 10% จริงๆแล้วสุทธิคือ -1% ไม่ใช่เท่าเดิม : (100% + 10%) x (100% - 10%) = 100% - 1%
2. แบ่งเงินออกเป็นสองส่วนเท่าๆกัน ส่วนแรกได้กำไร 10% ส่วนที่สองขาดทุน 10% ผลคือเท่าทุน : 50% x (100% + 10%) + 50% x (100% - 10%) = 100% + 0%
เพราะอะไร : เหตุผลคือ ความมั่งคั่งของเรา มีลักษณะ geometric ในแนว longitude และมีลักษณะ arithmetric ในแนว cross section นั่นเอง
ผมชอบมอง return ใน scale log เพราะมันมีคุณสมบัติ additivity ในช่วงเวลาต่างๆกัน
สมมติว่าเรา ได้กำไร 25% และขาดทุน 20% สุทธิคือ 1.25 x .8 = 1 นั่นคือ เท่าทุน ซึ่ง (0.25+ -0.2) <> 0 นั่นคือ ตัว return ไม่มี additivity
แต่หากลองเปลี่ยนมุมมองใหม่เป็น log return : ln(1.25)+ln(0.8) จะได้ว่า log return ของมันมี additivity, เหตุผล :
นอกจากจะมีคุณสมบัติ additivity แล้ว ยังมีสิ่งที่น่าสนใจอีกหลายประการ หนึ่งในนั้นก็คือ ในช่วงระยะสั้นๆ ที่ return ขนาดต่ำๆ ค่าของ log return จะใกล้เคียงกับค่าของ return
เหตุผล :
การที่มันเน้นย้ำฝั่งขาดทุน และลดทอนฝั่งกำไร ช่วยให้เรามองเห็นภาพพจน์ได้ชัดเจนขึ้น และช่วยรักษาคุณสมบัติ additivity ไว้ได้ และที่ขนาดน้อยๆ ค่าของมันค่อนข้างใกล้เคียงกับค่า return ปรกติ
อีกหนึ่งเหตุผลที่น่าสนใจ นั่นคือ สมมติฐานของโลกการเงินมักอยู่บน log normality จึงเป็นการสมเหตุผลผลมากกว่าหากเราจะใช้ log return
ทำไมนะหรือ ลองเปรียบเทียบ normality กับ log normality หากเรายอมรับ normality ก็หมายความว่า เรายอมรับว่าราคาหุ้นอาจขึ้นหรือตาม return แบบสุ่ม เช่นเดือนนี้อาจขึ้น 100% พรุ่งนี้ลง 120% ก็ได้
ในแต่ความเป็นจริง ไม่ได้ เพราะเราไม่ยอมรับราคาหุ้นที่ติดลบ หรือแม้กระทั้งเป็น 0
การที่เรายอมรับ log normality นั่นก็หมายถืง เรายอมรับราคาหุ้นที่เป็นบวกเท่านั้น เพราะ Exp(ln(1+R)) มีค่าเป็นบวกเสมอ นั่นคือ R > - 100% อยู่บนสมมติฐานที่ว่าราคาหุ้น จะไม่ถูกซื้อขายที่ 0 บาทหรือติดลบ
ทั้งนี้ทั้งนั้น ผมไม่ได้มาโปรโมทการใช้ scale log หรืออย่างไร แต่เพียงมาเสนอมุมมองดูครับ อาจเป็นประโยชน์ต่อเพื่อนๆนักลงทุน
สุดท้ายนี้ สวัสดีปีใหม่ ขอให้มีแต่สิ่งที่ดีงามเข้ามาในชีวิต คิดอะไรประสบสมหวังทุกประการครับผม