.
บทสรุปของแนวคิดแปลกใหม่บางส่วน
จากคณิตศาสตร์ และสมการทางคณิตศาสตร์
ที่เป็นกรอบแนวคิดที่มีลักษณะเฉพาะตัว
สมการเหล่านี้ทำให้เข้าใจถึงความเป็นจริง
และช่วยให้คนเรามองเห็นสิ่งต่าง ๆ
ที่ไม่เคยมีใครสังเกตมาก่อน
ดังนั้น จึงไม่น่าแปลกใจที่พัฒนาการใหม่ ๆ
ในวิชาคณิตศาสตร์ มักจะไปควบคู่กับ
ความก้าวหน้าในการทำความเข้าใจจักรวาล
9 สมการในประวัติศาสตร์
ที่ได้ปฏิวัติวิธีการมองทุกสิ่งทุกอย่าง
ตั้งแต่อนุภาคเล็ก ๆ จนถึงจักรวาลกว้างใหญ่
.
.
.
1.
Pythagorean theorem
.
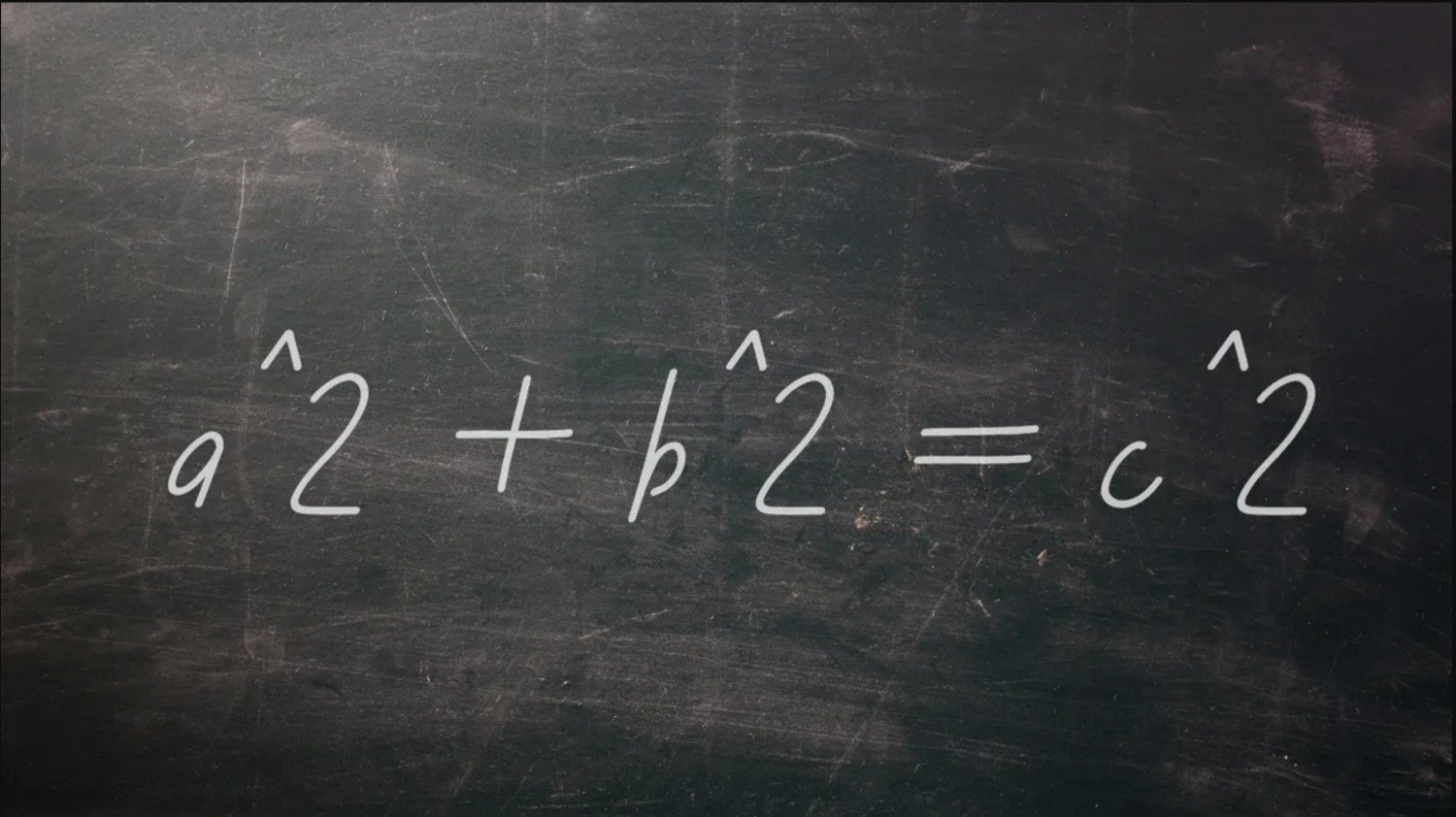
.
© Background: Eskay Lim
/ EyeEm via Getty Images
.
.
กฎตรีโกณมิติหลักประการแรกที่เรียนรู้กัน คือ
ความสัมพันธ์ระหว่างด้านของสามเหลี่ยมมุมฉาก
ความยาวของด้านที่สั้นกว่าทั้งสองด้านที่ยกกำลังสอง
แล้วบวกเข้าด้วยกัน จะเท่ากับ
ความยาวของด้านที่ยาวที่สุดที่ยกกำลังสอง
โดยปกติจะเขียนเป็น a^2 + b^2 = c^2
สมการนี้ที่รู้จักมาอย่างน้อย 3,700 ปี
นับตั้งแต่สมัยชาวบาบิโลนโบราณ
Pythagoras นักคณิตศาสตร์ชาวกรีก
ได้รับเกียรติในการเขียนสมการนี้
และยังใช้กันอยู่ในทุกวันนี้ ตามข้อมูลของ
University of St. Andrews ใน Scotland
ทฤษฎีบท Pythagorus ยังช่วยขยาย
ขอบเขตของสมการอีกด้วย
นอกจากการค้นหาความสูง
ยังมีการใช้งานในการก่อสร้าง
การนำทาง การทำแผนที่
และกระบวนการที่สำคัญอื่น ๆ
.
.

.
Pythagoras demonstrating
his Pythagorean theorem
in the sand using a stick
.
.
.
แนวคิดเรื่องตัวเลขของชาวกรีก
ในศตวรรษที่ 5 ก่อนคริสต์ศักราช
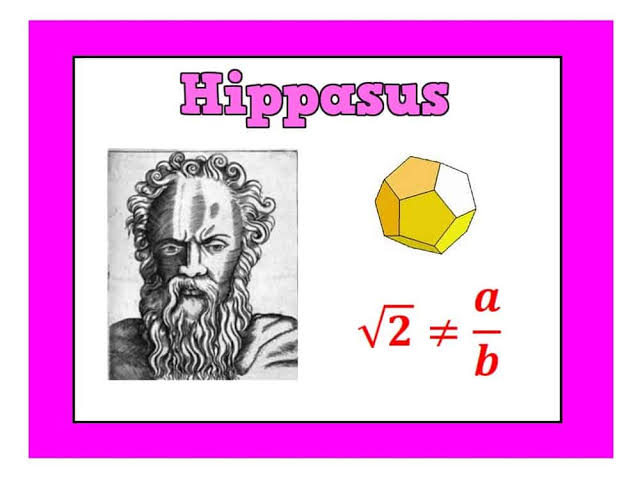
Hippasus of Metapontum
นักคณิตศาสตร์ สังเกตเห็นว่า
สามเหลี่ยมหน้าจั่ว
ซึ่งมีด้านฐานสองด้านยาว 1 หน่วย
จะมีด้านตรงข้ามมุมฉาก
ที่เป็นรากที่สองของ 2
ซึ่งเป็นจำนวนอตรรกยะ
ขัดแย้งความเชื่อดั้งเดิมของชาวกรีก
ที่เชื่อว่า เลข 1 3 5 7 9 คือ เลขคี่
2 4 6 8 คือ เลขคู่ จบกันแค่นี้ เพราะ
ทุกอย่าง คือ ตัวเลข All is number.
แต่การค้นพบตัวเลขจำนวนอตรรกยะ
ทำให้ชาวกรีก/นักคณิตศาสตร์หัวจะปวด
เพราะไม่รู้ว่า เมื่อใดตัวเลขจะจบจะสิ้น
มีตำนานเล่าว่า
การค้นพบครั้งนี้ของ Hippasus
ท่านจึงถูกจับโยนลงเล(ทะเล)เพื่อฆาตกรรม
เพราะสาวก Pythagoras รวมทั้ง Hippasus
รู้สึกไม่สบายใจกับความเป็นไปได้
ที่ตัวเลขอตรรกยะจะคงอยู่ตลอดไป
หลังจุดทศนิยมโดยไม่มีตัวเลขซ้ำกัน
ตามข้อมูล
University of Cambridge
.
.
.
2.
F = ma and the law of gravity
.
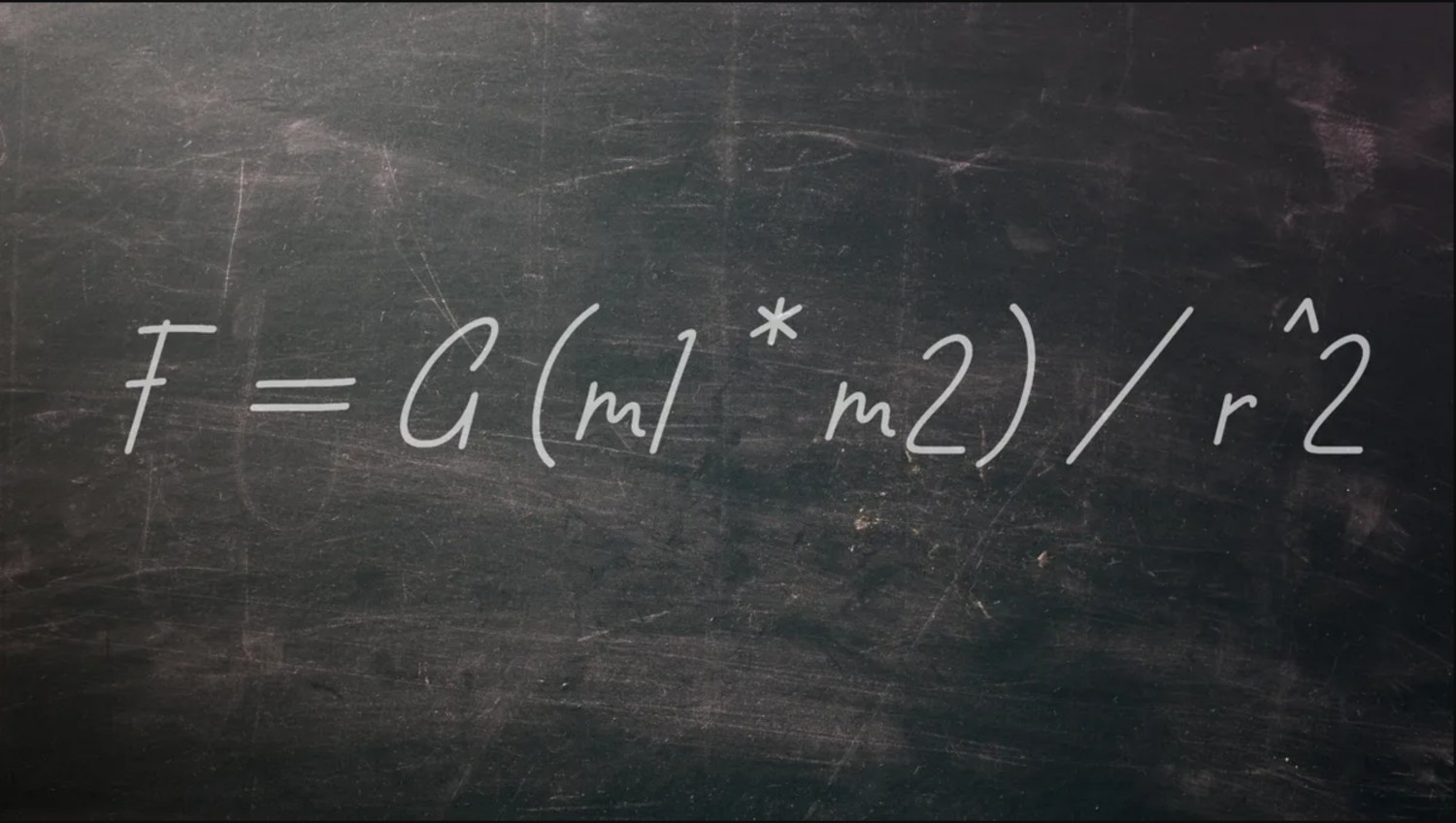
.
© Background: Eskay Lim
/ EyeEm via Getty Images
.
.
Sir Isaac Newton ราชบัณฑิตชาวอังกฤษ
ได้รับการยกย่องว่าเป็นผู้ค้นพบครั้งสำคัญ
ที่ทำให้โลกสั่นสะเทือนอย่างแรงมาก
หนึ่งในนั้น คือ กฎการเคลื่อนที่ข้อที่ 2
แรงมีค่าเท่ากับมวลของวัตถุคูณความเร่ง
ซึ่งปกติเขียนเป็น F = ma
การขยายกฎข้อนี้รวมกับข้อสังเกตอื่น ๆ
ทำให้ท่านอธิบายสิ่งที่ปัจจุบันเรียกว่า
กฎแรงโน้มถ่วงสากล ในปี 1687
โดยทั่วไปจะเขียนเป็น F = G (m1 * m2) / r^2
โดยที่ m1 และ m2 คือมวลของวัตถุ 2 ชิ้น
r คือระยะห่างระหว่างวัตถุทั้งสอง
G คือ ค่าคงที่พื้นฐานซึ่งจะต้องค้นหา
ค่าดังกล่าวนี้จากการทดลอง
แนวคิดเหล่านี้ถูกนำมาใช้
เพื่อทำความเข้าใจระบบทางกายภาพ
ในหลายระบบตั้งแต่นั้นเป็นต้นมา
รวมถึงการเคลื่อนที่ของดาวเคราะห์
ในระบบสุริยะจักรวาล และวิธีการเดินทาง
ในอวกาศ/ระหว่างทางด้วยจรวด
.
.
.
.
3.
The wave equation
.
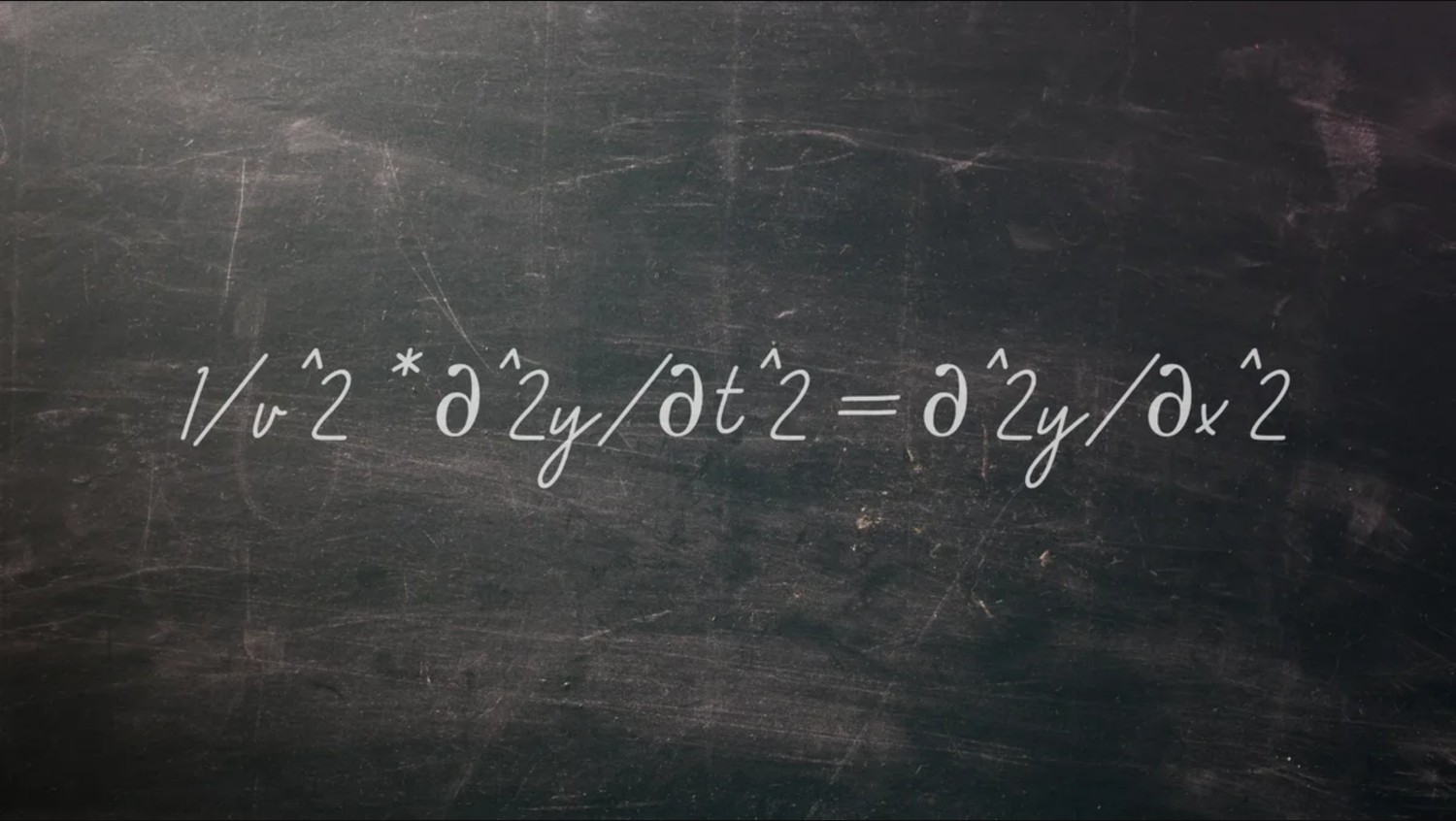
.
© Background: Eskay Lim
/ EyeEm via Getty Images
.
.
นักวิทยาศาสตร์ในศตวรรษที่ 18
เริ่มวิเคราะห์ทุกสิ่งรอบตัว
โดยใช้กฎที่ค่อนข้างใหม่
ของ Sir Isaac Newton
ในปี 1743
Jean-Baptiste le Rond d'Alembert
พหูสูต/ผู้รู้ชาวฝรั่งเศส
ได้มอบสมการที่อธิบายการสั่นสะเทือน
ของสายที่สั่น หรือการเคลื่อนที่ของคลื่น
ตามรายงานในวารสาร
Advances in Historical Studies
ที่สามารถเขียนสมการได้ดังนี้
1/v^2 * ∂^2y/∂t^2= ∂^2y/∂x^2
ในสมการนี้
v คือความเร็วของคลื่น และส่วนอื่น ๆ
อธิบายการกระจัดของคลื่นในทิศทางเดียว
สมการคลื่นขยายเป็นสองมิติขึ้นไป
ช่วยให้นักวิจัยทำนายการเคลื่อนที่ของน้ำ
แผ่นดินไหว คลื่นเสียง
และเป็นพื้นฐานของสิ่งต่าง ๆ
เช่น สมการ
Schrödinger
เรื่องฟิสิกส์ควอนตัม
ซึ่งเป็นรากฐานของ แกดเจ็ต Gadgets
ที่ใช้ในคอมพิวเตอร์ยุคใหม่จำนวนมาก
.
.
.
.
.
4.
Fourier’s equations
.
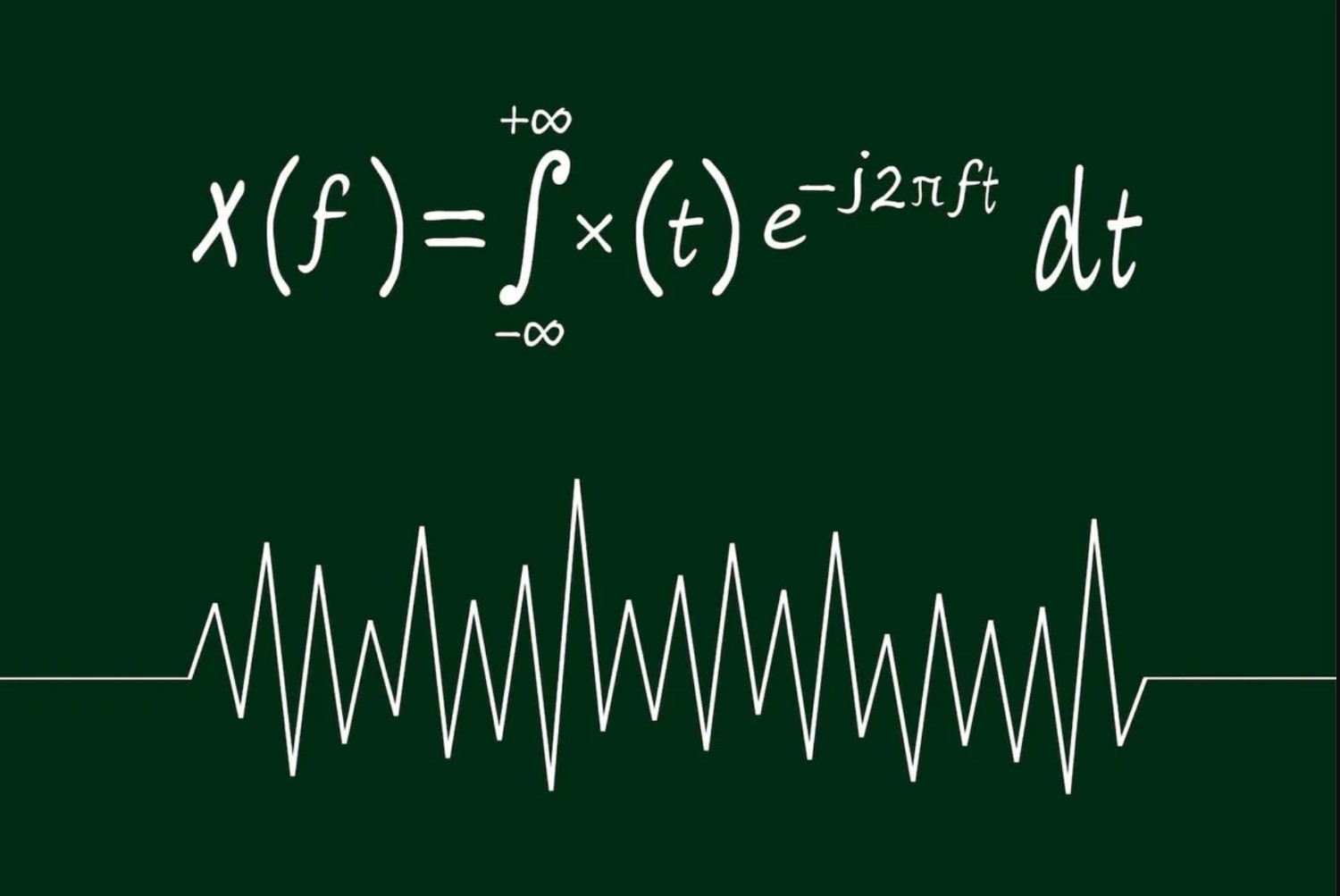
.
© Neslihan Gorucu/istock
/Getty Images Plus
.
.
แม้ว่าหลายคนอาจจะไม่เคยได้ยิน
เกี่ยวกับบารอนชาวฝรั่งเศส
Jean-Baptiste Joseph Fourier
แต่ผลงานของท่านได้ส่งผลกระทบ
ต่อชีวิตของคนเราเป็นอย่างมาก
นั่นเป็นเพราะสมการทางคณิตศาสตร์
ที่ท่านเขียนไว้ในปี 1822
ช่วยให้นักวิจัยสามารถแยกย่อยข้อมูล
ที่ซับซ้อนและยุ่งเหยิงออกมาเป็น
การรวมกันของคลื่นอย่างง่าย ๆ
ที่วิเคราะห์ได้ง่ายกว่ามาก
สมการสรุป Fourier นั้น
เป็นแนวคิดที่แตกต่างไปจากเดิม
อย่างสิ้นเชิงในยุคนั้นเพราะเรียบง่ายมาก
ทำให้นักวิทยาศาสตร์จำนวนมาก
ปฏิเสธเรื่องนี้และไม่เชื่อว่า
ระบบที่สลับซับซ้อนจะลดทอนลงได้
ให้กลายเป็นความเรียบง่ายที่สง่างามได้
ตามบทความใน
Yale Scientific
สมการสรุป Fourier เป็นตัวการขับเคลื่อน
ในสาขาวิทยาศาสตร์สมัยใหม่หลายแขนง
รวมถึงการประมวลผลข้อมูล
การวิเคราะห์ภาพ เลนส์ การสื่อสาร
ดาราศาสตร์ และวิศวกรรมศาสตร์
.
.

.
.
5.
Maxwell's equations
.

.
© ClaudeLux/istock/Getty Image Plus
.
.
ในช่วงทศวรรษปี 1800
ไฟฟ้าและแม่เหล็ก ยังคงเป็นแนวคิดใหม่
เมื่อนักวิชาการตรวจสอบว่า
จะจับและควบคุมพลังงาน
ประหลาดเหล่านี้ได้อย่างไร
James Clerk Maxwell
นักวิทยาศาสตร์ชาวสก็อต
ทำให้คนเราเข้าใจปรากฏการณ์
ทั้งสองอย่างนี้เพิ่มขึ้นอย่างมาก
ในปี 1864
ท่านได้ตีพิมพ์รายการสมการ 20 สมการ
ที่อธิบายว่าไฟฟ้าและแม่เหล็กเป็นอย่างไร
แม่เหล็กทำหน้าที่/มีความสัมพันธ์กับไฟฟ้า
ต่อมาสมการของท่านได้รับการสอน
ให้กับนักศึกษาฟิสิกส์ปีแรกในวิทยาลัย
และเป็นพื้นฐานสำหรับทุกสิ่งทุกอย่าง
ทางอิเล็กทรอนิกส์ในโลกเทคโนโลยีสมัยใหม่
.
.
.
.


9 สมการคณิตศาสตร์ที่เปลี่ยนโลก
บทสรุปของแนวคิดแปลกใหม่บางส่วน
จากคณิตศาสตร์ และสมการทางคณิตศาสตร์
ที่เป็นกรอบแนวคิดที่มีลักษณะเฉพาะตัว
สมการเหล่านี้ทำให้เข้าใจถึงความเป็นจริง
และช่วยให้คนเรามองเห็นสิ่งต่าง ๆ
ที่ไม่เคยมีใครสังเกตมาก่อน
ดังนั้น จึงไม่น่าแปลกใจที่พัฒนาการใหม่ ๆ
ในวิชาคณิตศาสตร์ มักจะไปควบคู่กับ
ความก้าวหน้าในการทำความเข้าใจจักรวาล
9 สมการในประวัติศาสตร์
ที่ได้ปฏิวัติวิธีการมองทุกสิ่งทุกอย่าง
ตั้งแต่อนุภาคเล็ก ๆ จนถึงจักรวาลกว้างใหญ่
.
.
1.
Pythagorean theorem
.
.
© Background: Eskay Lim
/ EyeEm via Getty Images
.
กฎตรีโกณมิติหลักประการแรกที่เรียนรู้กัน คือ
ความสัมพันธ์ระหว่างด้านของสามเหลี่ยมมุมฉาก
ความยาวของด้านที่สั้นกว่าทั้งสองด้านที่ยกกำลังสอง
แล้วบวกเข้าด้วยกัน จะเท่ากับ
ความยาวของด้านที่ยาวที่สุดที่ยกกำลังสอง
โดยปกติจะเขียนเป็น a^2 + b^2 = c^2
สมการนี้ที่รู้จักมาอย่างน้อย 3,700 ปี
นับตั้งแต่สมัยชาวบาบิโลนโบราณ
Pythagoras นักคณิตศาสตร์ชาวกรีก
ได้รับเกียรติในการเขียนสมการนี้
และยังใช้กันอยู่ในทุกวันนี้ ตามข้อมูลของ
University of St. Andrews ใน Scotland
ทฤษฎีบท Pythagorus ยังช่วยขยาย
ขอบเขตของสมการอีกด้วย
นอกจากการค้นหาความสูง
ยังมีการใช้งานในการก่อสร้าง
การนำทาง การทำแผนที่
และกระบวนการที่สำคัญอื่น ๆ
.
.
Pythagoras demonstrating
his Pythagorean theorem
in the sand using a stick
.
.
แนวคิดเรื่องตัวเลขของชาวกรีก
ในศตวรรษที่ 5 ก่อนคริสต์ศักราช
Hippasus of Metapontum
นักคณิตศาสตร์ สังเกตเห็นว่า
สามเหลี่ยมหน้าจั่ว
ซึ่งมีด้านฐานสองด้านยาว 1 หน่วย
จะมีด้านตรงข้ามมุมฉาก
ที่เป็นรากที่สองของ 2
ซึ่งเป็นจำนวนอตรรกยะ
ขัดแย้งความเชื่อดั้งเดิมของชาวกรีก
ที่เชื่อว่า เลข 1 3 5 7 9 คือ เลขคี่
2 4 6 8 คือ เลขคู่ จบกันแค่นี้ เพราะ
ทุกอย่าง คือ ตัวเลข All is number.
แต่การค้นพบตัวเลขจำนวนอตรรกยะ
ทำให้ชาวกรีก/นักคณิตศาสตร์หัวจะปวด
เพราะไม่รู้ว่า เมื่อใดตัวเลขจะจบจะสิ้น
มีตำนานเล่าว่า
การค้นพบครั้งนี้ของ Hippasus
ท่านจึงถูกจับโยนลงเล(ทะเล)เพื่อฆาตกรรม
เพราะสาวก Pythagoras รวมทั้ง Hippasus
รู้สึกไม่สบายใจกับความเป็นไปได้
ที่ตัวเลขอตรรกยะจะคงอยู่ตลอดไป
หลังจุดทศนิยมโดยไม่มีตัวเลขซ้ำกัน
ตามข้อมูล University of Cambridge
.
.
2.
F = ma and the law of gravity
.
.
© Background: Eskay Lim
/ EyeEm via Getty Images
.
Sir Isaac Newton ราชบัณฑิตชาวอังกฤษ
ได้รับการยกย่องว่าเป็นผู้ค้นพบครั้งสำคัญ
ที่ทำให้โลกสั่นสะเทือนอย่างแรงมาก
หนึ่งในนั้น คือ กฎการเคลื่อนที่ข้อที่ 2
แรงมีค่าเท่ากับมวลของวัตถุคูณความเร่ง
ซึ่งปกติเขียนเป็น F = ma
การขยายกฎข้อนี้รวมกับข้อสังเกตอื่น ๆ
ทำให้ท่านอธิบายสิ่งที่ปัจจุบันเรียกว่า
กฎแรงโน้มถ่วงสากล ในปี 1687
โดยทั่วไปจะเขียนเป็น F = G (m1 * m2) / r^2
โดยที่ m1 และ m2 คือมวลของวัตถุ 2 ชิ้น
r คือระยะห่างระหว่างวัตถุทั้งสอง
G คือ ค่าคงที่พื้นฐานซึ่งจะต้องค้นหา
ค่าดังกล่าวนี้จากการทดลอง
แนวคิดเหล่านี้ถูกนำมาใช้
เพื่อทำความเข้าใจระบบทางกายภาพ
ในหลายระบบตั้งแต่นั้นเป็นต้นมา
รวมถึงการเคลื่อนที่ของดาวเคราะห์
ในระบบสุริยะจักรวาล และวิธีการเดินทาง
ในอวกาศ/ระหว่างทางด้วยจรวด
.
.
.
3.
The wave equation
.
.
© Background: Eskay Lim
/ EyeEm via Getty Images
.
นักวิทยาศาสตร์ในศตวรรษที่ 18
เริ่มวิเคราะห์ทุกสิ่งรอบตัว
โดยใช้กฎที่ค่อนข้างใหม่
ของ Sir Isaac Newton
ในปี 1743
Jean-Baptiste le Rond d'Alembert
พหูสูต/ผู้รู้ชาวฝรั่งเศส
ได้มอบสมการที่อธิบายการสั่นสะเทือน
ของสายที่สั่น หรือการเคลื่อนที่ของคลื่น
ตามรายงานในวารสาร
Advances in Historical Studies
ที่สามารถเขียนสมการได้ดังนี้
1/v^2 * ∂^2y/∂t^2= ∂^2y/∂x^2
ในสมการนี้
v คือความเร็วของคลื่น และส่วนอื่น ๆ
อธิบายการกระจัดของคลื่นในทิศทางเดียว
สมการคลื่นขยายเป็นสองมิติขึ้นไป
ช่วยให้นักวิจัยทำนายการเคลื่อนที่ของน้ำ
แผ่นดินไหว คลื่นเสียง
และเป็นพื้นฐานของสิ่งต่าง ๆ
เช่น สมการ Schrödinger
เรื่องฟิสิกส์ควอนตัม
ซึ่งเป็นรากฐานของ แกดเจ็ต Gadgets
ที่ใช้ในคอมพิวเตอร์ยุคใหม่จำนวนมาก
.
.
.
.
4.
Fourier’s equations
.
.
© Neslihan Gorucu/istock
/Getty Images Plus
.
แม้ว่าหลายคนอาจจะไม่เคยได้ยิน
เกี่ยวกับบารอนชาวฝรั่งเศส
Jean-Baptiste Joseph Fourier
แต่ผลงานของท่านได้ส่งผลกระทบ
ต่อชีวิตของคนเราเป็นอย่างมาก
นั่นเป็นเพราะสมการทางคณิตศาสตร์
ที่ท่านเขียนไว้ในปี 1822
ช่วยให้นักวิจัยสามารถแยกย่อยข้อมูล
ที่ซับซ้อนและยุ่งเหยิงออกมาเป็น
การรวมกันของคลื่นอย่างง่าย ๆ
ที่วิเคราะห์ได้ง่ายกว่ามาก
สมการสรุป Fourier นั้น
เป็นแนวคิดที่แตกต่างไปจากเดิม
อย่างสิ้นเชิงในยุคนั้นเพราะเรียบง่ายมาก
ทำให้นักวิทยาศาสตร์จำนวนมาก
ปฏิเสธเรื่องนี้และไม่เชื่อว่า
ระบบที่สลับซับซ้อนจะลดทอนลงได้
ให้กลายเป็นความเรียบง่ายที่สง่างามได้
ตามบทความใน Yale Scientific
สมการสรุป Fourier เป็นตัวการขับเคลื่อน
ในสาขาวิทยาศาสตร์สมัยใหม่หลายแขนง
รวมถึงการประมวลผลข้อมูล
การวิเคราะห์ภาพ เลนส์ การสื่อสาร
ดาราศาสตร์ และวิศวกรรมศาสตร์
.
.
.
5.
Maxwell's equations
.
.
© ClaudeLux/istock/Getty Image Plus
.
ในช่วงทศวรรษปี 1800
ไฟฟ้าและแม่เหล็ก ยังคงเป็นแนวคิดใหม่
เมื่อนักวิชาการตรวจสอบว่า
จะจับและควบคุมพลังงาน
ประหลาดเหล่านี้ได้อย่างไร
James Clerk Maxwell
นักวิทยาศาสตร์ชาวสก็อต
ทำให้คนเราเข้าใจปรากฏการณ์
ทั้งสองอย่างนี้เพิ่มขึ้นอย่างมาก
ในปี 1864
ท่านได้ตีพิมพ์รายการสมการ 20 สมการ
ที่อธิบายว่าไฟฟ้าและแม่เหล็กเป็นอย่างไร
แม่เหล็กทำหน้าที่/มีความสัมพันธ์กับไฟฟ้า
ต่อมาสมการของท่านได้รับการสอน
ให้กับนักศึกษาฟิสิกส์ปีแรกในวิทยาลัย
และเป็นพื้นฐานสำหรับทุกสิ่งทุกอย่าง
ทางอิเล็กทรอนิกส์ในโลกเทคโนโลยีสมัยใหม่
.
.