คำตอบที่ได้รับเลือกจากเจ้าของกระทู้
ความคิดเห็นที่ 2
หลักการสำคัญคือ เส้นสัมผัสย่อมตั้งฉากกับรัศมี ณ จุดสัมผัส จากนั้นก็ใช้ความรู้เรื่องสามเหลี่ยมคล้ายกับทฤษฎีบทพีทาโกรัส ก็จะหาคำตอบได้ ตามรายละเอียดในกรณีทั่วไปดังต่อไปนี้นะครับ
1. กรณีที่จุดสัมผัสอยู่คนละด้านของส่วนของเส้นตรง PQ

จากรูป จะเห็นว่าสามเหลี่ยม PAX คล้ายกับสามเหลี่ยม QBX เนื่องจากเราทราบว่า PA = รัศมีของวงกลม P, QB = รัศมีของวงกลม Q และทราบความยาว PQ ดังนั้นจะสามารถหาระยะ PX ได้โดยใช้หลักการของสามเหลี่ยมคล้าย กล่าวคือจะได้สมการ PA/QB = PX/(PQ - PX) [สังเกตว่า QX = PQ - PX] ซึ่งเมื่อแก้สมการนี้ ก็จะได้ความยาว PX และ QX จากนั้นก็ใช้ทฤษฎีบทพีทาโกรัส ทำให้เราหาความยาว AX, ความยาว BX และหาความยาว AB = AX + BX ได้ในที่สุด
2. กรณีที่จุดสัมผัสอยู่ด้านเดียวกันของส่วนของเส้นตรง PQ
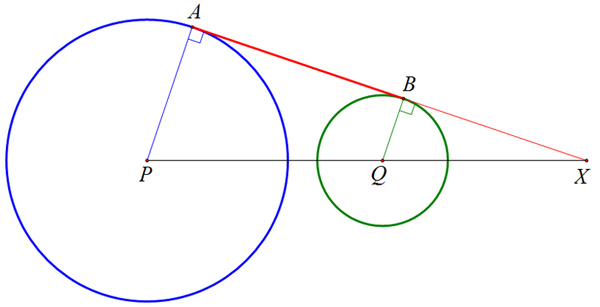
จากรูป จะเห็นว่าสามเหลี่ยม PAX คล้ายกับสามเหลี่ยม QBX จากหลักการของสามเหลี่ยมคล้าย จะได้สมการ PA/QB = PX/(PX - PQ) [สังเกตว่า QX = PX - PQ] ซึ่งเมื่อแก้สมการนี้ ก็จะได้ความยาว PX และ QX จากนั้นก็ใช้ทฤษฎีบทพีทาโกรัส ทำให้เราหาความยาว AX, ความยาว BX และหาความยาว AB = AX - BX ได้ในที่สุด
1. กรณีที่จุดสัมผัสอยู่คนละด้านของส่วนของเส้นตรง PQ

จากรูป จะเห็นว่าสามเหลี่ยม PAX คล้ายกับสามเหลี่ยม QBX เนื่องจากเราทราบว่า PA = รัศมีของวงกลม P, QB = รัศมีของวงกลม Q และทราบความยาว PQ ดังนั้นจะสามารถหาระยะ PX ได้โดยใช้หลักการของสามเหลี่ยมคล้าย กล่าวคือจะได้สมการ PA/QB = PX/(PQ - PX) [สังเกตว่า QX = PQ - PX] ซึ่งเมื่อแก้สมการนี้ ก็จะได้ความยาว PX และ QX จากนั้นก็ใช้ทฤษฎีบทพีทาโกรัส ทำให้เราหาความยาว AX, ความยาว BX และหาความยาว AB = AX + BX ได้ในที่สุด
2. กรณีที่จุดสัมผัสอยู่ด้านเดียวกันของส่วนของเส้นตรง PQ

จากรูป จะเห็นว่าสามเหลี่ยม PAX คล้ายกับสามเหลี่ยม QBX จากหลักการของสามเหลี่ยมคล้าย จะได้สมการ PA/QB = PX/(PX - PQ) [สังเกตว่า QX = PX - PQ] ซึ่งเมื่อแก้สมการนี้ ก็จะได้ความยาว PX และ QX จากนั้นก็ใช้ทฤษฎีบทพีทาโกรัส ทำให้เราหาความยาว AX, ความยาว BX และหาความยาว AB = AX - BX ได้ในที่สุด
แสดงความคิดเห็น


ช่วยทำโจทย์เรขาคณิตหน่อยครับ
2.ถ้าวงกลมPมีรัศมี 8 นิ้ววงกลม Q มีรัศมี 3 นิ้วโดยที่ส่วนของเส้นตรง P Q ยาว 13 นิ้วแล้วเส้นสัมผัสร่วม AB (ซึ่ง A และ B อยู่บนด้านเดียวกันของเส้นตรง PQ) ยาวกี่นิ้ว