จากโจทย์จะได้รายละเอียดดังรูป


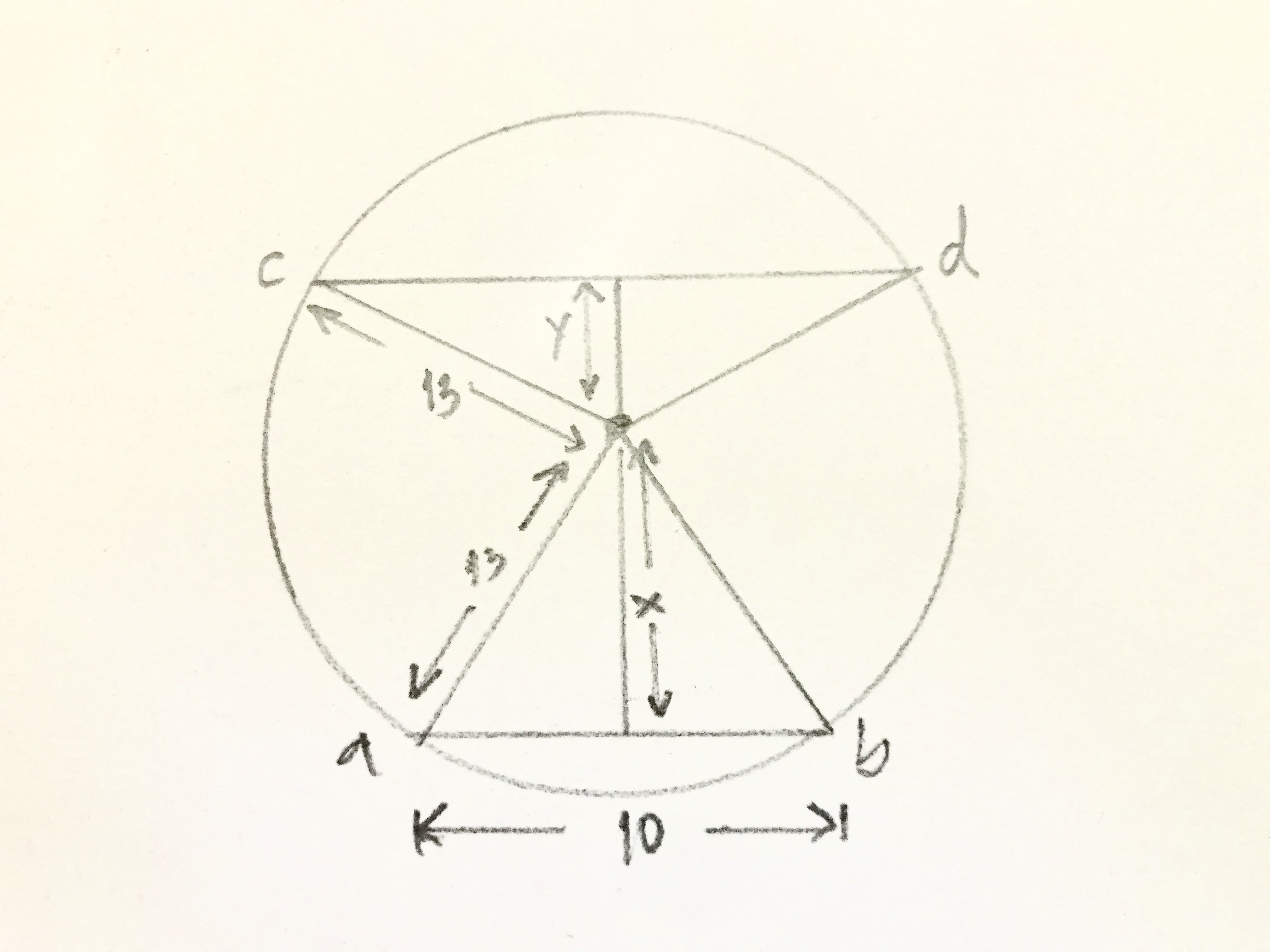
จากรูป จะได้ว่า X + Y = 17 ...... (1)

รัศมีของวงกลม = 13 เมื่อลากเส้นตรงจากปลายทั้ง 2 ข้างของคอร์ด ab จะได้รูปสามเหลี่ยม ที่มีความสูงเท่ากับ X

1. แก้สมการหาความสูง X

จากทฤษฎีบทพีทาโกรัส a² + b² = c² จะได้ว่า

X² + (ab/2)² = 13²
X² + 5² = 13²
X² + 25 = 169
X² = 169 - 25
X² = 144
X = 12

แทนค่า X ใน (1) จะได้ว่า

12 + Y = 17
Y = 17 - 12
Y = 5

เมื่อลากเส้นตรงจากปลายทั้ง 2 ข้างของคอร์ด cd จะได้รูปสามเหลี่ยม ที่มีความสูงเท่ากับ Y

2. แก้สมการหา cd

จากทฤษฎีบทพีทาโกรัส a² + b² = c² จะได้ว่า

Y² + (cd/2)² = 13²
5² + (cd/2)² = 13²
25 + (cd/2)² = 169
(cd/2)² = 169 - 25
(cd/2)² = 144
(cd/2) = 12
cd = 12 x 2
cd = 24