☭

☭
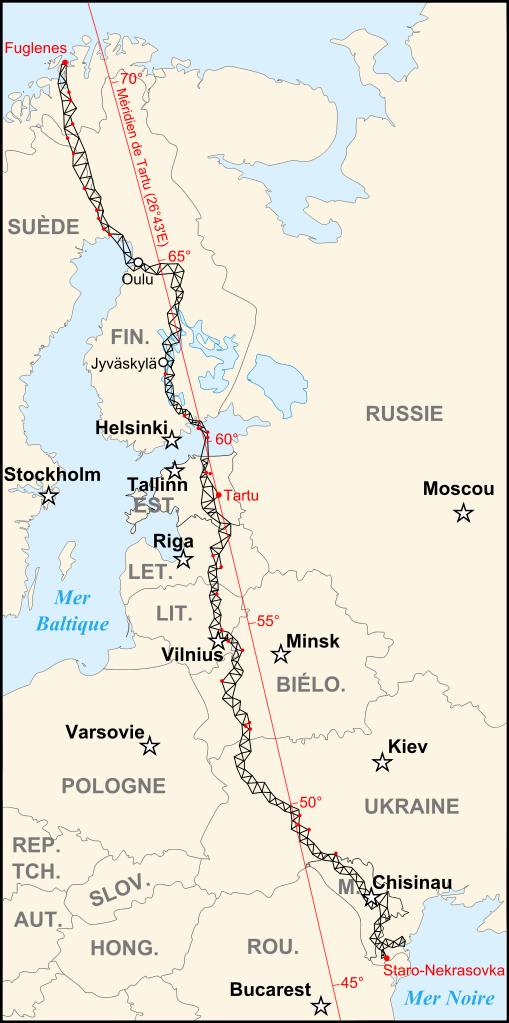
สถานีเหนือสุดของ Struve Geodetic Arc
ตั้งอยู่ในเมือง Fuglenes ประเทศนอร์เวย์
© Francesco Bandarin / Wikimedia
☭
☭
จากชายฝั่งทางเหนือของนอร์เวย์
ไปจนถึงชายฝั่งทางตอนใต้ของยูเครน
มีจุดสามเหลี่ยมแบบสำรวจรวมกันเป็น Struve Geodetic Arc
ทอดยาวจาก Hammerfest (Norway)
บนชายฝั่งมหาสมุทรอาร์กติก Arctic Ocean
ไปจนถึง Nekrasivka (Ukraine) ใกล้ทะเลดำ Black Sea
ระยะทางยาว 2,820 กิโลเมตร
ซึ่งเส้นที่จะผ่านเข้า/ออกจากดินแดนมากมาย
ซึ่งปัจจุบันอยู่ในสิบประเทศที่แตกต่างกัน
ส่วนโค้งนี้ก่อตั้งโดยนักวิทยาศาสตร์เยอรมันในรัสเซียชื่อ
Friedrich Georg Wilhelm von Struve
ซึ่งทำการสำรวจเป็นเวลา 39 ปีระหว่างปี 1816 - 1855
เพื่อกำหนดรูปร่างและขนาดของโลก
การสำรวจให้ผลการวัดที่แม่นยำครั้งแรก
ของส่วนโค้งเมริดียน meridian arc
ทำให้สามารถวัดเส้นผ่านศูนย์กลางของโลก
ได้อย่างแม่นยำในครั้งแรกในโลก
☭
☭
☭
☭
การกำหนดขนาดและรูปร่างของโลก
เป็นหนึ่งในปัญหาที่สำคัญที่สุดสำหรับ
นักปรัชญาธรรมชาติตั้งแต่สมัยโบราณ
ในศตวรรษที่ 2 ก่อนคริสตกาล
นักดาราศาสตร์และนักคณิตศาสตร์
ชาวกรีก
Eratosthenes
ได้พัฒนาวิธีการกำหนดรัศมีของโลก
โดยการวัดส่วนหนึ่งของเส้นเมริเดียน
และเปรียบเทียบความยาวนั้นกับมุม
ที่สอดคล้องกันซึ่งกำหนดไว้ที่ศูนย์กลางของโลก
หากรู้ความยาวส่วนโค้งและมุมศูนย์กลาง
รัศมีสามารถคำนวณได้ง่าย
☭
☭

☭
Eratosthenes กำลังสอน Alexandria
โดย Bernardo Strozzi (1635)
☭
☭
Eratosthenes คำนวณความยาวส่วนโค้ง
ด้วยเส้นเมริเดียน 1 องศา ที่ผ่าน
เมือง Alexandria กับ Siena (Aswan ตอนใต้ Egypt)
ความยาวเส้น S เป็นไปตามสูตร S = 2πR 360°S
เส้นรัศมี R มาจากการวัดเวลาที่กองคาราวานข้ามทะเลทราย
ส่วนโค้งถูกกำหนดโดยการวัดความแตกต่าง
ระหว่างความสูงของดวงอาทิตย์ระหว่างละติจูด
แม้ว่าความแม่นยำในการวัดของเขาจะต่ำ
แต่ Eratosthenes ก็สามารถคำนวณรัศมี
ของโลกด้วยความแม่นยำที่คลาดเคลื่อน 1%
ใช้กันมายาวนานเป็นเวลา 2,000 ปี
ที่ วิธีการสังเกตระดับ ของ Eratosthenes
ยังคงเป็นวิธีการที่มีแนวโน้มมากที่สุด
ในการกำหนดขนาดของโลก
แต่สิ่งที่ดีขึ้นคือ วิธีการวัดในเวลาต่อมา
☭
☭
☭
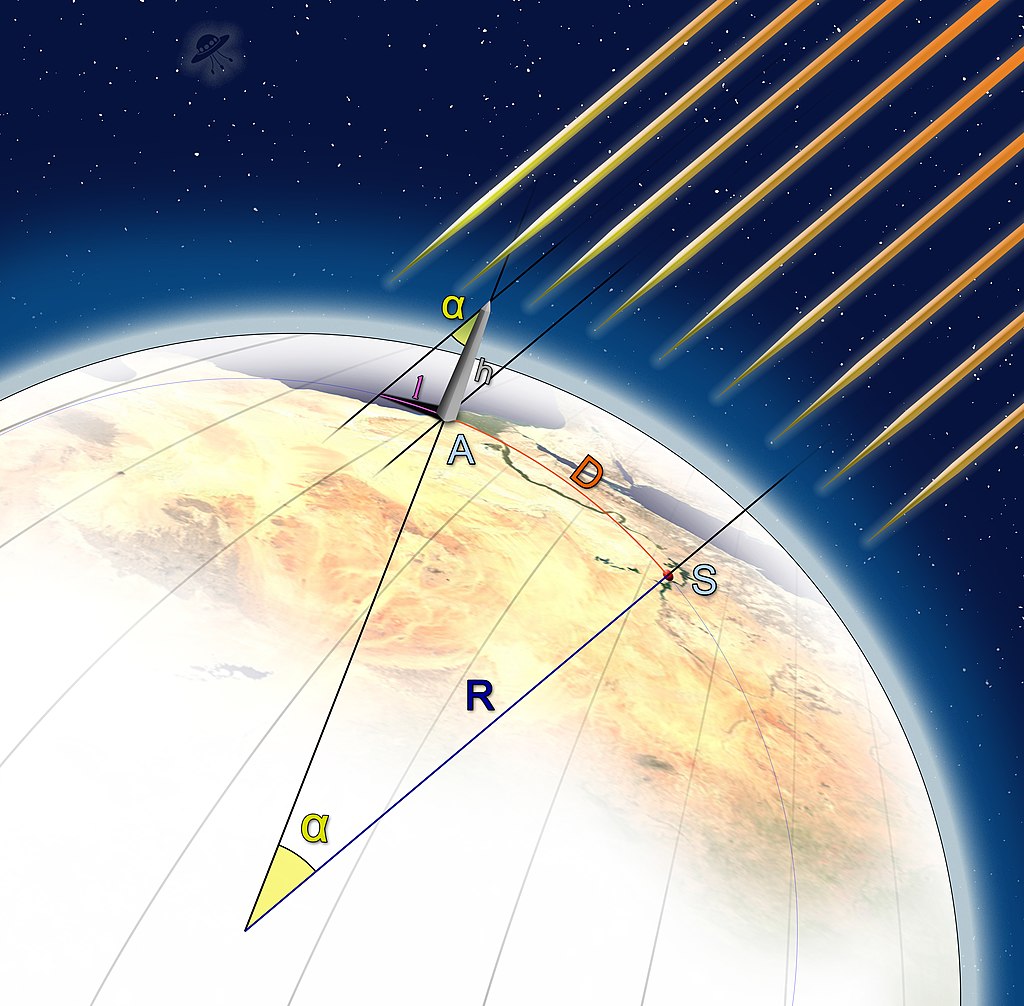
Measure of Earth's circumference according
to Cleomedes' simplified version
based on the approximation that Syene
is on the Tropic of Cancer and on
the same meridian as Alexandria
☭
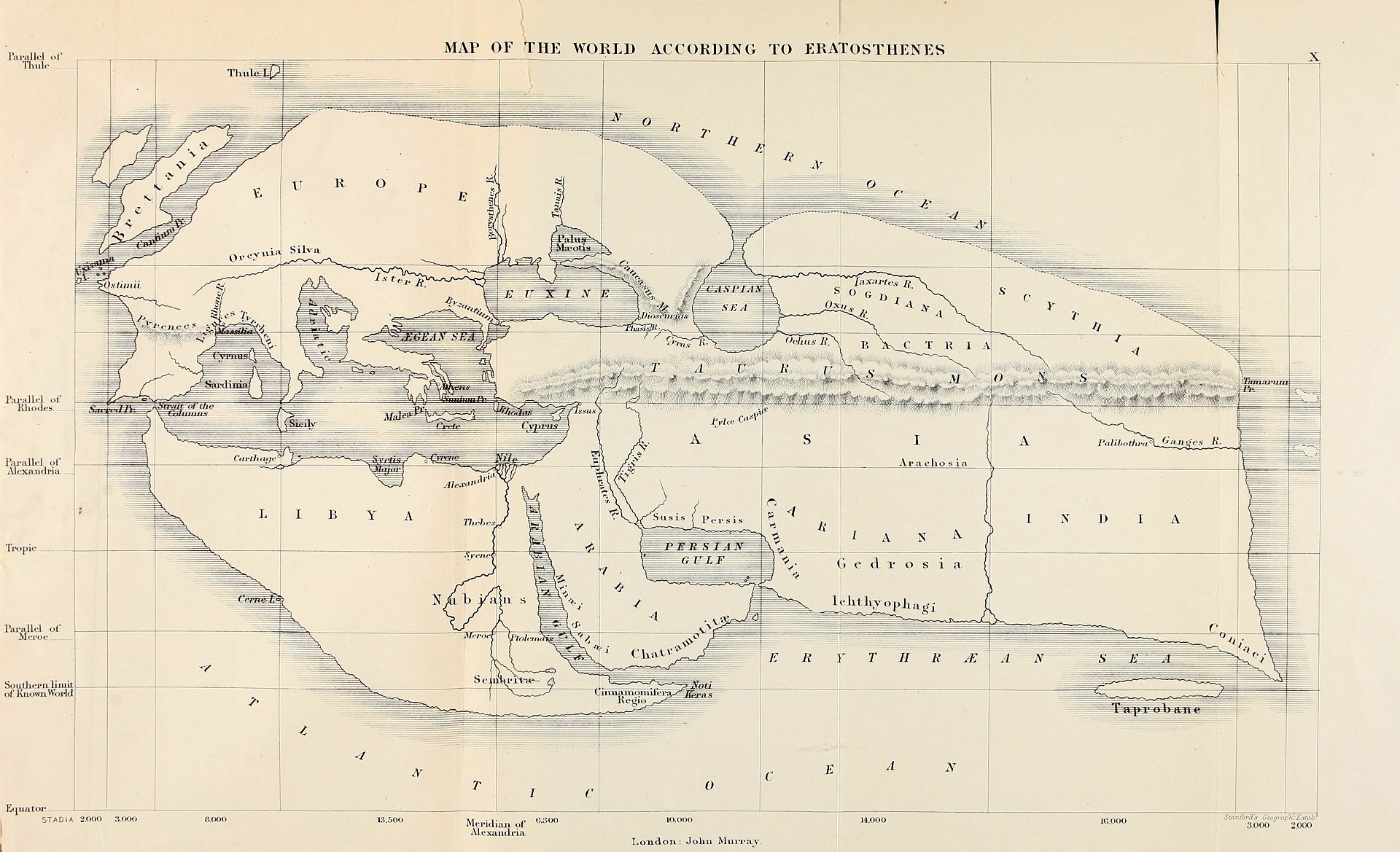
☭
19th century reconstruction of Eratosthenes
map of the (for the Greeks) known world, c. 194 BC
☭
☭

☭
☭
เพื่อกำหนดรัศมีของโลกได้แม่นยำยิ่งขึ้น
จึงต้องดำเนินการวัด Geodetic ที่แม่นยำยิ่งขึ้น
จุดเปลี่ยนที่แท้จริงในการเสริมสร้าง
วิธีการวัดพื้นผิวโลกที่แม่นยำนั้น
เกิดขึ้นในเวลาต่อมามาก ในคริสต์ศตวรรษที่ 17
เมื่อ
Willebrord Snellius นักธรณีวิทยาชาวดัตช์
เสนอให้ใช้วิธีการที่เรียกว่า Triangulation
ในขณะที่ Isaac Newton ในปี 1687 ได้พิสูจน์ว่า
รูปร่างของโลกหมุนบนแกนของโลกคล้ายกับทรงรี
หมายความว่า รัศมีความโค้งของโลก
ที่เคลื่อนจากเส้นศูนย์สูตรไปยังขั้วโลกควรเพิ่มขึ้น
โดยใช้วิธีการสามเหลี่ยมเพื่อกำหนดระยะห่าง
ระหว่างจุดต่าง ๆ บนพื้นผิวโลก
โดยเชื่อมโยงเข้าด้วยกันเป็นระบบสามเหลี่ยม
วัดมุมของสามเหลี่ยมและอย่างน้อยหนึ่งด้าน - ฐาน
☭
☭

☭
Snellius' Triangulation (1615)
☭
☭
เทคนิคการวัดแบบใหม่ที่เรียกว่า Triangulation
ได้รับการพัฒนาโดยใช้การวัดระยะทางสั้น ๆ อย่างแม่นยำ
ในขณะที่ระยะทางไกลสามารถกำหนดได้
โดยใช้สายโซ่ของรูปสามเหลี่ยมที่เชื่อมต่อกัน
การหาสามเหลี่ยมช่วยให้นักดาราศาสตร์
และนักทำแผนที่สามารถวัดระยะทางไกล
ที่ทอดยาวเป็นระยะทางไกลมาก
หลายร้อยหลายพันกิโลเมตรได้อย่างแม่นยำ
☭
☭

☭
Quadrant of Snellius
© Museum Boerhaave, Leiden
☭

☭
Portrait of Isaac Newton (1642-1727)
☭
☭

☭
Georg Wilhelm von Struve (1793–1864)
☭
☭
ในช่วงศตวรรษที่ 18
มีการสร้างส่วนโค้งหลายแห่งทั่วยุโรป
แต่ส่วนโค้งของ
Friedrich Georg Wilhelm von Struve
ชาวรัสเซียเชื้อสายเยอรมัน
ที่มีการนำเข้ามาพัฒนารัสเซียตั้งแต่สมัย
จักรพรรดินีนาถเยกาเจรีนามหาราชินี
ทึ่มาจากราชวงศ์ปรัสเซีย(เยอรมัน)
ท่านเป็นศาสตราจารย์แห่งมหาวิทยาลัย Tartu
และหัวหน้าหอดูดาวดาราศาสตร์ของมหาวิทยาลัย
ได้จัดระบบผลการวัดที่เลือกของเศษส่วน
ของเครือข่ายรูปสามเหลี่ยม
เพื่อคำนวณเส้นเมอริเดียนของ Arcand
ที่บรรยายไว้ใน รายงานสุดท้าย Arc du Méridien de 25°20'
จากงานนี้โดย F. G. W. von Struve ในปี 1888
ความยาวของเส้นเมอริเดียนของโลก
คำนวณโดยนักธรณีวิทยา I. Bonsdorff
ส่วนโค้งที่ยาวที่สุดเมื่อสร้างขึ้น
และยังคงอยู่เป็นเวลานานกว่าศตวรรษ
นอกจากนี้ยังเป็นการวัดที่แม่นยำที่สุด
โดยให้การวัดที่ลดลงเพียง 4 มม. ต่อทุกๆ 1 กม.
กล่าวอีกนัยหนึ่งโดยใช้ส่วนโค้งของท่าน
รัศมีของโลกคำนวณได้แตกต่าง 223 เมตรจากของจริง
Struve Geodetic Arc เป็นห่วงโซ่
การวัดรูปสามเหลี่ยมที่เกิดขึ้นในปี 1816–1852
ซึ่งทอดยาวจากลองจิจูด 26° ตะวันออก
ไปตามเส้นเมอริเดียนจากแฮมเมอร์เฟสต์ (นอร์เวย์)
บนชายฝั่งมหาสมุทรอาร์กติกถึงอิสมาอิล (ยูเครน) ริมทะเลดำ
กล่าวคือ จาก 4 °20' ถึง 70°40' ละติจูดเหนือ
The Arc ครอบคลุม 10 ชาติในปัจจุบัน
ในช่วงเวลาของการสร้าง
ส่วนโค้งได้ผ่านสองประเทศ ได้แก่
สหภาพสวีเดน-นอร์เวย์ และจักรวรรดิรัสเซีย
แต่การเปลี่ยนแปลงในขอบเขตทางการเมือง
หลังการล่มสลายของสหภาพโซเวียต-รัสเซีย
ทำให้เกิดประเทศเล็กประเทศน้อยตามมา
ได้ทำให้จุดต่างๆ กระจัดกระจายไปทั่ว 10 ประเทศ
ได้แก่ นอร์เวย์ สวีเดน ฟินแลนด์ รัสเซีย เอสโตเนีย
ลัตเวีย ลิทัวเนีย เบลารุส ยูเครน และมอลดาเวีย
ความยาวและตำแหน่งของเส้นเมอริเดียนอาร์ค
คำนวณโดยชิ้นส่วนเครือข่ายสามเหลี่ยมที่วัดได้ในประเทศดังกล่าว
การเชื่อมต่อเข้าด้วยกันส่งผลให้เกิดสายโซ่ยาว 2,822 กม.
ประกอบด้วย 12 ส่วนซึ่งกระจายอยู่ระหว่างจุดดาราศาสตร์
มีฐานที่วัดได้ 10 ฐาน สามเหลี่ยม 258 รูปและเชื่อมต่อจุดสามเหลี่ยม 259 จุด
ความยาวเฉลี่ยของด้านข้างของรูปสามเหลี่ยมคือ 27 กม.
แต่มีด้านยาวกว่า 50 กม. ความแตกต่างของละติจูดทางภูมิศาสตร์
ของจุดสิ้นสุดของห่วงโซ่นี้มีค่าเท่ากับ 25°20’
แม้ว่าการวัดจะดำเนินการในสภาวะที่ซับซ้อน
แต่งาน geodetic ก็ดำเนินการได้อย่างแม่นยำอย่างน่าประหลาดใจ
ข้อผิดพลาดในการวัดมุมเฉลี่ยไม่ถึง 0.7”
ในขณะที่ความแม่นยำของความยาวส่วนโค้งคือ 1/232390 (4 มม. ต่อกม.)
☭
☭
☭
☭
จนถึงกลางปี ค.ศ. 2000
มีการใช้ Geodetic ด้วยดาวเทียมเป็นครั้งแรก
นี่เป็นส่วนโค้งที่วัดได้อย่างแม่นยำ/ยาวที่สุด
ตลอดศตวรรษผลลัพธ์ของการวัดในครั้งนั้น
ได้ถูกนำมาใช้ในการคำนวณ
และปรับพารามิเตอร์ของทรงรีของโลก
จุดบนห่วงโซ่รูปสามเหลี่ยมนั้น
มีทั้งทำด้วยหินในทุ่งนาที่ฝังไว้
ผูกไว้กับปูนขาวในบ่อที่ขุด
ที่หินด้านบนเจาะรู หลุมนั้นเต็มไปด้วยตะกั่ว
และกากบาทถูกทำเครื่องหมายไว้ตรงกลาง
ทางตอนเหนือของ Struve Geodetic Arc
จุดศูนย์กลางของจุดรูปสามเหลี่ยม
มักถูกทำเครื่องหมายด้วยหินแข็ง
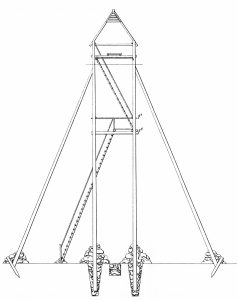
สำหรับการวัดมุม ปิรามิดไม้ (เสารูปสามเหลี่ยม)
ถูกสร้างขึ้นที่จุด สูงถึง 50 เมตร ในบางสถานที่
อุปกรณ์ออปติคัลถูกใช้ในการวัดมุมระหว่างจุดต่าง ๆ
โดยใช้วัตถุท้องฟ้า ละติจูดทางดาราศาสตร์
และมุมแอซิมัททางดาราศาสตร์ของทิศทาง
ที่มุ่งไปยังจุดใกล้เคียงถูกกำหนด
โดยวัตถุท้องฟ้า ที่ฐาน - ความยาวของเส้น
☭
☭

☭
A Struve Geodetic Arc station in Latvia
© Jānis U./Wikimedia
☭
☭

☭
A Struve Geodetic Arc station in Hogland, Russia
© Islander/Wikimedia
☭
☭

☭
A Struve Geodetic Arc station in Alta, Norway
© aoiaio/Wikimedia
☭
☭

☭
A Struve Geodetic Arc marker at Tartu Old Observatory in Tartu
© Graham Stone/Flickr
☭
☭

☭
A Struve Geodetic Arc station in Lithuania
© Stefan Krasowski/Flickr
☭
☭
Struve Geodetic Arc เส้น 2,820 กม. ที่วัดขนาดโลกได้อย่างแม่นยำ
☭
สถานีเหนือสุดของ Struve Geodetic Arc
ตั้งอยู่ในเมือง Fuglenes ประเทศนอร์เวย์
© Francesco Bandarin / Wikimedia
☭
จากชายฝั่งทางเหนือของนอร์เวย์
ไปจนถึงชายฝั่งทางตอนใต้ของยูเครน
มีจุดสามเหลี่ยมแบบสำรวจรวมกันเป็น Struve Geodetic Arc
ทอดยาวจาก Hammerfest (Norway)
บนชายฝั่งมหาสมุทรอาร์กติก Arctic Ocean
ไปจนถึง Nekrasivka (Ukraine) ใกล้ทะเลดำ Black Sea
ระยะทางยาว 2,820 กิโลเมตร
ซึ่งเส้นที่จะผ่านเข้า/ออกจากดินแดนมากมาย
ซึ่งปัจจุบันอยู่ในสิบประเทศที่แตกต่างกัน
ส่วนโค้งนี้ก่อตั้งโดยนักวิทยาศาสตร์เยอรมันในรัสเซียชื่อ
Friedrich Georg Wilhelm von Struve
ซึ่งทำการสำรวจเป็นเวลา 39 ปีระหว่างปี 1816 - 1855
เพื่อกำหนดรูปร่างและขนาดของโลก
การสำรวจให้ผลการวัดที่แม่นยำครั้งแรก
ของส่วนโค้งเมริดียน meridian arc
ทำให้สามารถวัดเส้นผ่านศูนย์กลางของโลก
ได้อย่างแม่นยำในครั้งแรกในโลก
☭
☭
การกำหนดขนาดและรูปร่างของโลก
เป็นหนึ่งในปัญหาที่สำคัญที่สุดสำหรับ
นักปรัชญาธรรมชาติตั้งแต่สมัยโบราณ
ในศตวรรษที่ 2 ก่อนคริสตกาล
นักดาราศาสตร์และนักคณิตศาสตร์
ชาวกรีก Eratosthenes
ได้พัฒนาวิธีการกำหนดรัศมีของโลก
โดยการวัดส่วนหนึ่งของเส้นเมริเดียน
และเปรียบเทียบความยาวนั้นกับมุม
ที่สอดคล้องกันซึ่งกำหนดไว้ที่ศูนย์กลางของโลก
หากรู้ความยาวส่วนโค้งและมุมศูนย์กลาง
รัศมีสามารถคำนวณได้ง่าย
☭
☭
Eratosthenes กำลังสอน Alexandria
โดย Bernardo Strozzi (1635)
☭
Eratosthenes คำนวณความยาวส่วนโค้ง
ด้วยเส้นเมริเดียน 1 องศา ที่ผ่าน
เมือง Alexandria กับ Siena (Aswan ตอนใต้ Egypt)
ความยาวเส้น S เป็นไปตามสูตร S = 2πR 360°S
เส้นรัศมี R มาจากการวัดเวลาที่กองคาราวานข้ามทะเลทราย
ส่วนโค้งถูกกำหนดโดยการวัดความแตกต่าง
ระหว่างความสูงของดวงอาทิตย์ระหว่างละติจูด
แม้ว่าความแม่นยำในการวัดของเขาจะต่ำ
แต่ Eratosthenes ก็สามารถคำนวณรัศมี
ของโลกด้วยความแม่นยำที่คลาดเคลื่อน 1%
ใช้กันมายาวนานเป็นเวลา 2,000 ปี
ที่ วิธีการสังเกตระดับ ของ Eratosthenes
ยังคงเป็นวิธีการที่มีแนวโน้มมากที่สุด
ในการกำหนดขนาดของโลก
แต่สิ่งที่ดีขึ้นคือ วิธีการวัดในเวลาต่อมา
☭
☭
Measure of Earth's circumference according
to Cleomedes' simplified version
based on the approximation that Syene
is on the Tropic of Cancer and on
the same meridian as Alexandria
☭
☭
19th century reconstruction of Eratosthenes
map of the (for the Greeks) known world, c. 194 BC
☭
☭
☭
เพื่อกำหนดรัศมีของโลกได้แม่นยำยิ่งขึ้น
จึงต้องดำเนินการวัด Geodetic ที่แม่นยำยิ่งขึ้น
จุดเปลี่ยนที่แท้จริงในการเสริมสร้าง
วิธีการวัดพื้นผิวโลกที่แม่นยำนั้น
เกิดขึ้นในเวลาต่อมามาก ในคริสต์ศตวรรษที่ 17
เมื่อ Willebrord Snellius นักธรณีวิทยาชาวดัตช์
เสนอให้ใช้วิธีการที่เรียกว่า Triangulation
ในขณะที่ Isaac Newton ในปี 1687 ได้พิสูจน์ว่า
รูปร่างของโลกหมุนบนแกนของโลกคล้ายกับทรงรี
หมายความว่า รัศมีความโค้งของโลก
ที่เคลื่อนจากเส้นศูนย์สูตรไปยังขั้วโลกควรเพิ่มขึ้น
โดยใช้วิธีการสามเหลี่ยมเพื่อกำหนดระยะห่าง
ระหว่างจุดต่าง ๆ บนพื้นผิวโลก
โดยเชื่อมโยงเข้าด้วยกันเป็นระบบสามเหลี่ยม
วัดมุมของสามเหลี่ยมและอย่างน้อยหนึ่งด้าน - ฐาน
☭
☭
Snellius' Triangulation (1615)
☭
เทคนิคการวัดแบบใหม่ที่เรียกว่า Triangulation
ได้รับการพัฒนาโดยใช้การวัดระยะทางสั้น ๆ อย่างแม่นยำ
ในขณะที่ระยะทางไกลสามารถกำหนดได้
โดยใช้สายโซ่ของรูปสามเหลี่ยมที่เชื่อมต่อกัน
การหาสามเหลี่ยมช่วยให้นักดาราศาสตร์
และนักทำแผนที่สามารถวัดระยะทางไกล
ที่ทอดยาวเป็นระยะทางไกลมาก
หลายร้อยหลายพันกิโลเมตรได้อย่างแม่นยำ
☭
☭
Quadrant of Snellius
© Museum Boerhaave, Leiden
☭
☭
Portrait of Isaac Newton (1642-1727)
☭
☭
☭
Georg Wilhelm von Struve (1793–1864)
☭
ในช่วงศตวรรษที่ 18
มีการสร้างส่วนโค้งหลายแห่งทั่วยุโรป
แต่ส่วนโค้งของ Friedrich Georg Wilhelm von Struve
ชาวรัสเซียเชื้อสายเยอรมัน
ที่มีการนำเข้ามาพัฒนารัสเซียตั้งแต่สมัย
จักรพรรดินีนาถเยกาเจรีนามหาราชินี
ทึ่มาจากราชวงศ์ปรัสเซีย(เยอรมัน)
ท่านเป็นศาสตราจารย์แห่งมหาวิทยาลัย Tartu
และหัวหน้าหอดูดาวดาราศาสตร์ของมหาวิทยาลัย
ได้จัดระบบผลการวัดที่เลือกของเศษส่วน
ของเครือข่ายรูปสามเหลี่ยม
เพื่อคำนวณเส้นเมอริเดียนของ Arcand
ที่บรรยายไว้ใน รายงานสุดท้าย Arc du Méridien de 25°20'
จากงานนี้โดย F. G. W. von Struve ในปี 1888
ความยาวของเส้นเมอริเดียนของโลก
คำนวณโดยนักธรณีวิทยา I. Bonsdorff
ส่วนโค้งที่ยาวที่สุดเมื่อสร้างขึ้น
และยังคงอยู่เป็นเวลานานกว่าศตวรรษ
นอกจากนี้ยังเป็นการวัดที่แม่นยำที่สุด
โดยให้การวัดที่ลดลงเพียง 4 มม. ต่อทุกๆ 1 กม.
กล่าวอีกนัยหนึ่งโดยใช้ส่วนโค้งของท่าน
รัศมีของโลกคำนวณได้แตกต่าง 223 เมตรจากของจริง
Struve Geodetic Arc เป็นห่วงโซ่
การวัดรูปสามเหลี่ยมที่เกิดขึ้นในปี 1816–1852
ซึ่งทอดยาวจากลองจิจูด 26° ตะวันออก
ไปตามเส้นเมอริเดียนจากแฮมเมอร์เฟสต์ (นอร์เวย์)
บนชายฝั่งมหาสมุทรอาร์กติกถึงอิสมาอิล (ยูเครน) ริมทะเลดำ
กล่าวคือ จาก 4 °20' ถึง 70°40' ละติจูดเหนือ
The Arc ครอบคลุม 10 ชาติในปัจจุบัน
ในช่วงเวลาของการสร้าง
ส่วนโค้งได้ผ่านสองประเทศ ได้แก่
สหภาพสวีเดน-นอร์เวย์ และจักรวรรดิรัสเซีย
แต่การเปลี่ยนแปลงในขอบเขตทางการเมือง
หลังการล่มสลายของสหภาพโซเวียต-รัสเซีย
ทำให้เกิดประเทศเล็กประเทศน้อยตามมา
ได้ทำให้จุดต่างๆ กระจัดกระจายไปทั่ว 10 ประเทศ
ได้แก่ นอร์เวย์ สวีเดน ฟินแลนด์ รัสเซีย เอสโตเนีย
ลัตเวีย ลิทัวเนีย เบลารุส ยูเครน และมอลดาเวีย
ความยาวและตำแหน่งของเส้นเมอริเดียนอาร์ค
คำนวณโดยชิ้นส่วนเครือข่ายสามเหลี่ยมที่วัดได้ในประเทศดังกล่าว
การเชื่อมต่อเข้าด้วยกันส่งผลให้เกิดสายโซ่ยาว 2,822 กม.
ประกอบด้วย 12 ส่วนซึ่งกระจายอยู่ระหว่างจุดดาราศาสตร์
มีฐานที่วัดได้ 10 ฐาน สามเหลี่ยม 258 รูปและเชื่อมต่อจุดสามเหลี่ยม 259 จุด
ความยาวเฉลี่ยของด้านข้างของรูปสามเหลี่ยมคือ 27 กม.
แต่มีด้านยาวกว่า 50 กม. ความแตกต่างของละติจูดทางภูมิศาสตร์
ของจุดสิ้นสุดของห่วงโซ่นี้มีค่าเท่ากับ 25°20’
แม้ว่าการวัดจะดำเนินการในสภาวะที่ซับซ้อน
แต่งาน geodetic ก็ดำเนินการได้อย่างแม่นยำอย่างน่าประหลาดใจ
ข้อผิดพลาดในการวัดมุมเฉลี่ยไม่ถึง 0.7”
ในขณะที่ความแม่นยำของความยาวส่วนโค้งคือ 1/232390 (4 มม. ต่อกม.)
☭
จนถึงกลางปี ค.ศ. 2000
มีการใช้ Geodetic ด้วยดาวเทียมเป็นครั้งแรก
นี่เป็นส่วนโค้งที่วัดได้อย่างแม่นยำ/ยาวที่สุด
ตลอดศตวรรษผลลัพธ์ของการวัดในครั้งนั้น
ได้ถูกนำมาใช้ในการคำนวณ
และปรับพารามิเตอร์ของทรงรีของโลก
จุดบนห่วงโซ่รูปสามเหลี่ยมนั้น
มีทั้งทำด้วยหินในทุ่งนาที่ฝังไว้
ผูกไว้กับปูนขาวในบ่อที่ขุด
ที่หินด้านบนเจาะรู หลุมนั้นเต็มไปด้วยตะกั่ว
และกากบาทถูกทำเครื่องหมายไว้ตรงกลาง
ทางตอนเหนือของ Struve Geodetic Arc
จุดศูนย์กลางของจุดรูปสามเหลี่ยม
มักถูกทำเครื่องหมายด้วยหินแข็ง
สำหรับการวัดมุม ปิรามิดไม้ (เสารูปสามเหลี่ยม)
ถูกสร้างขึ้นที่จุด สูงถึง 50 เมตร ในบางสถานที่
อุปกรณ์ออปติคัลถูกใช้ในการวัดมุมระหว่างจุดต่าง ๆ
โดยใช้วัตถุท้องฟ้า ละติจูดทางดาราศาสตร์
และมุมแอซิมัททางดาราศาสตร์ของทิศทาง
ที่มุ่งไปยังจุดใกล้เคียงถูกกำหนด
โดยวัตถุท้องฟ้า ที่ฐาน - ความยาวของเส้น
☭
A Struve Geodetic Arc station in Latvia
© Jānis U./Wikimedia
☭
☭
☭
A Struve Geodetic Arc station in Hogland, Russia
© Islander/Wikimedia
☭
☭
☭
A Struve Geodetic Arc station in Alta, Norway
© aoiaio/Wikimedia
☭
☭
☭
A Struve Geodetic Arc marker at Tartu Old Observatory in Tartu
© Graham Stone/Flickr
☭
☭
☭
A Struve Geodetic Arc station in Lithuania
© Stefan Krasowski/Flickr
☭
☭