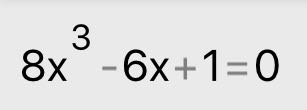
สมการนี้ มาจากการที่ผมอยากจะหาค่าของ sin10 (sin ของมุม 10 องศา) ครับ

จากเอกลักษณ์ด้านบน แทน a = 10 องศา แล้วให้ sin10 = x จะได้สมการตามหัวกระทู้ ก็คือ 8x^3 - 6x + 1 = 0
มีใครสามารถแก้สมการนี้ แล้วได้คำตอบในรูป Exact Form บ้างครับ (แบบ
ไม่ใช่ค่าประมาณแล้วก็ไม่วนมาเป็นรูป sin 10 องศาเหมือนเดิม)
ผมลองแก้ด้วยสูตรคาร์ดานแล้ว แต่มันเกิดข้อขัดแย้ง (ได้คำตอบเป็นจำนวนจินตภาพ)
เพราะถ้าสามารถหาค่า x ซึ่งก็คือ sin10 ได้ ก็จะสามารถหา sin ได้ทุกมุมโดยที่มุมเป็นจำนวนเต็ม (sin1 = sin(10-9) , sin9 = sqrt((1-cos18)/2) พอได้ sin1 ก็เหมือนได้ sin ของทุกมุมในรูป Exact Form) รบกวนผู้รู้ด้วยครับ ขอบคุณครับ
ปล. ที่ผมลองทำเองมันแปลกๆครับ

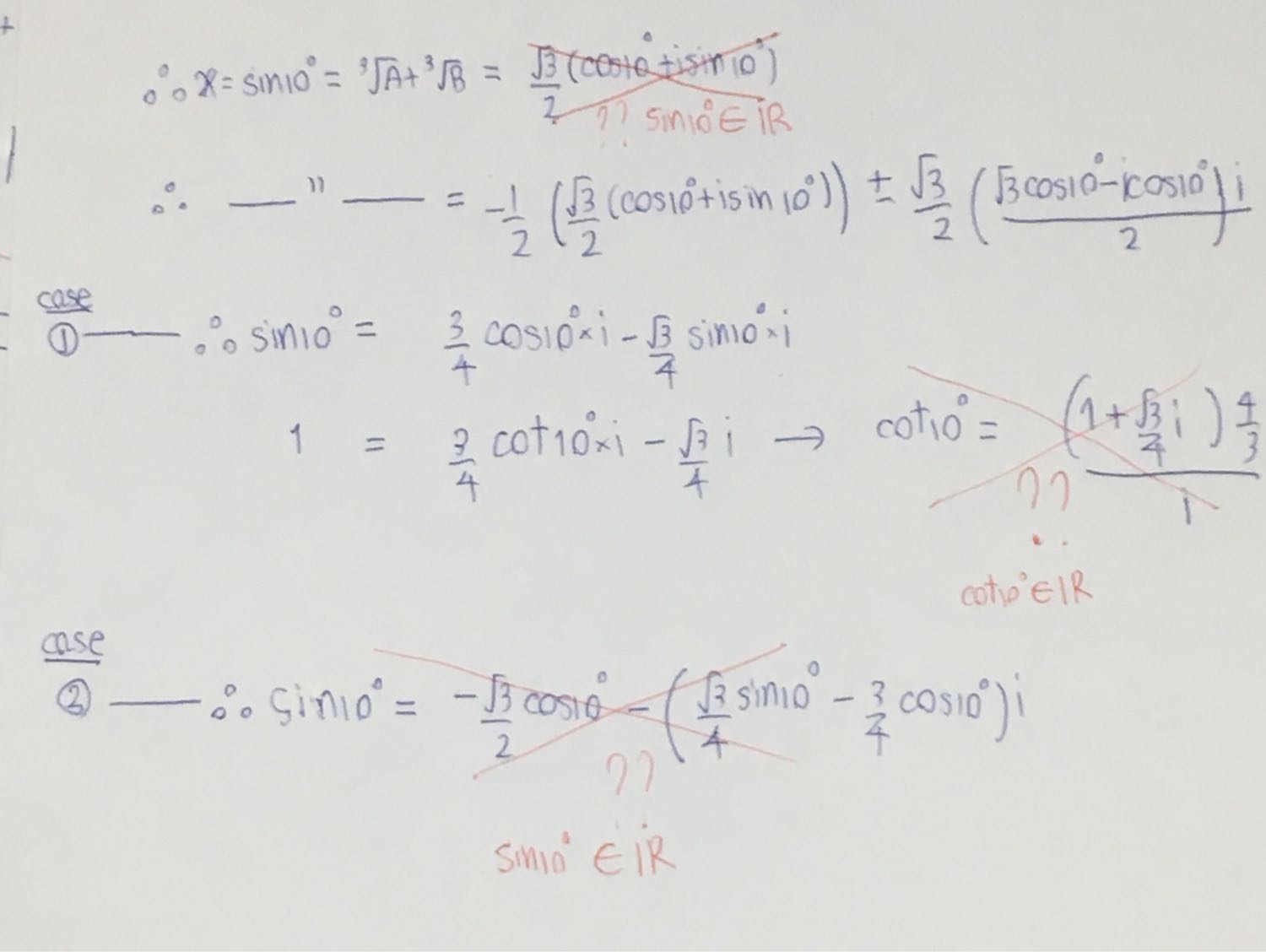
คำตอบของสมการ 8x^3 - 6x + 1 = 0 ในรูป Exact Form
สมการนี้ มาจากการที่ผมอยากจะหาค่าของ sin10 (sin ของมุม 10 องศา) ครับ
จากเอกลักษณ์ด้านบน แทน a = 10 องศา แล้วให้ sin10 = x จะได้สมการตามหัวกระทู้ ก็คือ 8x^3 - 6x + 1 = 0
มีใครสามารถแก้สมการนี้ แล้วได้คำตอบในรูป Exact Form บ้างครับ (แบบไม่ใช่ค่าประมาณแล้วก็ไม่วนมาเป็นรูป sin 10 องศาเหมือนเดิม)
ผมลองแก้ด้วยสูตรคาร์ดานแล้ว แต่มันเกิดข้อขัดแย้ง (ได้คำตอบเป็นจำนวนจินตภาพ)
เพราะถ้าสามารถหาค่า x ซึ่งก็คือ sin10 ได้ ก็จะสามารถหา sin ได้ทุกมุมโดยที่มุมเป็นจำนวนเต็ม (sin1 = sin(10-9) , sin9 = sqrt((1-cos18)/2) พอได้ sin1 ก็เหมือนได้ sin ของทุกมุมในรูป Exact Form) รบกวนผู้รู้ด้วยครับ ขอบคุณครับ
ปล. ที่ผมลองทำเองมันแปลกๆครับ