สุดยอดความคิดเห็น
ความคิดเห็นที่ 3
ขั้นตอนต่อไป
การหาค่า x
[Spoil] คลิกเพื่อดูข้อความที่ซ่อนไว้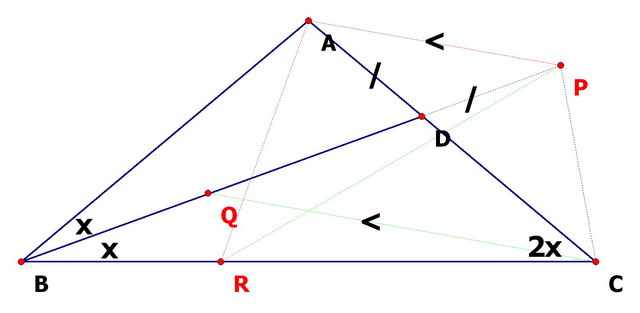
สร้างเพื่อการหาค่า
1. ต่อส่วนของเส้นตรง AD ไปถึง P ที่ทำให้ DP = AD
2. ลากเส้นตรง AP และ CP
3. จากจุด C ลากเส้นตรง CQ ขนานกับเส้น AP และไปตัดกับเส้นตรง BP ที่จุด Q
4. กำหนดจุด R บนเส้นตรง BC ที่ทำให้ CR = AC
5. ลากเส้นตรง AR
การหาค่า x
จาก มุม ADB = 2x + x = 3x และด้าน AD = DP
ดังนั้น มุม DAP = มุม DPA = 3x/2 ………….[1]
จาก AD = DP และ AD + BD = BC
ดังนั้น DP + BD = BC --> BP = BC ……….[2]
ทำให้ มุม BCP = มุม BPC = (180-x)/2 = 90 – x/2 ……… [3]
จาก Lemma 1 ที่กำหนดมาก่อนหน้านี้
จะได้ว่า AB:BC = AD:CD
จาก CQ // AP --> สามเหลี่ยม ADP คล้ายกับ สามเหลี่ยม CDQ
AD:CD = AP:CQ
ทำให้ AB:BC = AP:CQ ……………………………..[4]
จาก CA = CR --> มุม CAR = มุม CRA = (180-2x)/2 = 90-x …. [5]
มุม PAR = มุม CAR + มุม CAP = 90-x + 3x/2 (จาก [5] และ [1])
= 90 + x/2 ………………………….. [6]
ดังนั้น มุม PAR + มุม PCR (PCB) = (90 + x/2) + (90 – x/2) (จาก [6] และ [3])
= 180 องศา
ทำให้ APCR เป็นสี่เหลี่ยมในวงกลม
ดังนั้น มุม APR = มุม ACR (เป็นมุมบน segment เดียวกัน) = 2x ……[7]
พิจารณา สามเหลี่ยม BPR และสามเหลี่ยม BCQ
จะได้ว่า BP = BC (จาก [2]) …………….. ##
มุม PBR = มุม CBQ (เป็นมุมเดียวกัน) ……..##
มุม BPR = มุม APR – มุม DPA = 2x – 3x/2 (จาก [7] และ [1])
= x/2
มุม BCQ = มุม ACB – มุม ACQ = 2x – 3x/2 (มุม ACQ = มุม DAP เพราะ CQ // AP)
= x/2
มุม BPR = มุม BCQ …………………….##
จาก ## จะได้ สามเหลี่ยม BPR และสามเหลี่ยม BCQ เป็นสามเหลี่ยมเท่ากันทุกประการ
ดังนั้น PR = CQ …………………. [8]
พิจารณา สามเหลี่ยม ABC และสามเหลี่ยม APR
มุม ABC = มุม APR = 2x ………. @
AB : BC = AP : PR (จาก [4] และ [8])
ทำให้ AB : AP = BC : PR ………….@
จาก Lemma 2 ที่ได้พิสูจน์ไปก่อนหน้านี้แล้ว และ @
จะได้ว่า สามเหลี่ยม ABC และสามเหลี่ยม APR เป็นสามเหลี่ยมคล้าย
ดังนั้น มุม BAC = มุม PAR
มุม BAC = 180-4x, มุม PAR = 90+x/2 (จาก [6])
ทำให้ 180-4x = 90 + x/2
จะได้ x = 20 องศา
** ของแถม เรายังพิสูจน์ต่อได้ว่า สามเหลี่ยม BAR และ CAP เป็นสามเหลี่ยมเท่ากันทุกประการ
AQ = BQ = BR = CP และ จุด A, P, C, R. Q อยู่บนวงกลมเดียวกัน **
กว่าผมจะพิมพ์เสร็จ ใช้เวลาหลายชั่วโมง
การหาค่า x
[Spoil] คลิกเพื่อดูข้อความที่ซ่อนไว้

สร้างเพื่อการหาค่า
1. ต่อส่วนของเส้นตรง AD ไปถึง P ที่ทำให้ DP = AD
2. ลากเส้นตรง AP และ CP
3. จากจุด C ลากเส้นตรง CQ ขนานกับเส้น AP และไปตัดกับเส้นตรง BP ที่จุด Q
4. กำหนดจุด R บนเส้นตรง BC ที่ทำให้ CR = AC
5. ลากเส้นตรง AR
การหาค่า x
จาก มุม ADB = 2x + x = 3x และด้าน AD = DP
ดังนั้น มุม DAP = มุม DPA = 3x/2 ………….[1]
จาก AD = DP และ AD + BD = BC
ดังนั้น DP + BD = BC --> BP = BC ……….[2]
ทำให้ มุม BCP = มุม BPC = (180-x)/2 = 90 – x/2 ……… [3]
จาก Lemma 1 ที่กำหนดมาก่อนหน้านี้
จะได้ว่า AB:BC = AD:CD
จาก CQ // AP --> สามเหลี่ยม ADP คล้ายกับ สามเหลี่ยม CDQ
AD:CD = AP:CQ
ทำให้ AB:BC = AP:CQ ……………………………..[4]
จาก CA = CR --> มุม CAR = มุม CRA = (180-2x)/2 = 90-x …. [5]
มุม PAR = มุม CAR + มุม CAP = 90-x + 3x/2 (จาก [5] และ [1])
= 90 + x/2 ………………………….. [6]
ดังนั้น มุม PAR + มุม PCR (PCB) = (90 + x/2) + (90 – x/2) (จาก [6] และ [3])
= 180 องศา
ทำให้ APCR เป็นสี่เหลี่ยมในวงกลม
ดังนั้น มุม APR = มุม ACR (เป็นมุมบน segment เดียวกัน) = 2x ……[7]
พิจารณา สามเหลี่ยม BPR และสามเหลี่ยม BCQ
จะได้ว่า BP = BC (จาก [2]) …………….. ##
มุม PBR = มุม CBQ (เป็นมุมเดียวกัน) ……..##
มุม BPR = มุม APR – มุม DPA = 2x – 3x/2 (จาก [7] และ [1])
= x/2
มุม BCQ = มุม ACB – มุม ACQ = 2x – 3x/2 (มุม ACQ = มุม DAP เพราะ CQ // AP)
= x/2
มุม BPR = มุม BCQ …………………….##
จาก ## จะได้ สามเหลี่ยม BPR และสามเหลี่ยม BCQ เป็นสามเหลี่ยมเท่ากันทุกประการ
ดังนั้น PR = CQ …………………. [8]
พิจารณา สามเหลี่ยม ABC และสามเหลี่ยม APR
มุม ABC = มุม APR = 2x ………. @
AB : BC = AP : PR (จาก [4] และ [8])
ทำให้ AB : AP = BC : PR ………….@
จาก Lemma 2 ที่ได้พิสูจน์ไปก่อนหน้านี้แล้ว และ @
จะได้ว่า สามเหลี่ยม ABC และสามเหลี่ยม APR เป็นสามเหลี่ยมคล้าย
ดังนั้น มุม BAC = มุม PAR
มุม BAC = 180-4x, มุม PAR = 90+x/2 (จาก [6])
ทำให้ 180-4x = 90 + x/2
จะได้ x = 20 องศา
** ของแถม เรายังพิสูจน์ต่อได้ว่า สามเหลี่ยม BAR และ CAP เป็นสามเหลี่ยมเท่ากันทุกประการ
AQ = BQ = BR = CP และ จุด A, P, C, R. Q อยู่บนวงกลมเดียวกัน **
กว่าผมจะพิมพ์เสร็จ ใช้เวลาหลายชั่วโมง
ลองลิ้มรส ลองแล้วรัก ซึ้ง, ลูกไหน ทึ่ง, นมสดใส่หน้านม ทึ่ง, หอยทากติดเทอร์โบ ทึ่ง, amdintel ทึ่ง, สมาชิกหมายเลข 761866 ทึ่ง, เต้าหู้ตกกระ ถูกใจ, หางแหลม ทึ่ง, sawatcafe ถูกใจ, TIYHz ทึ่งรวมถึงอีก 10 คน ร่วมแสดงความรู้สึก
▼ กำลังโหลดข้อมูล... ▼
แสดงความคิดเห็น
คุณสามารถแสดงความคิดเห็นกับกระทู้นี้ได้ด้วยการเข้าสู่ระบบ
กระทู้ที่คุณอาจสนใจ
อ่านกระทู้อื่นที่พูดคุยเกี่ยวกับ
คณิตศาสตร์


โจทย์เก่าของคุณ TIYHz กระทู้ 30636714 แต่ผมขอตอบ
ค่าของ x เท่ากับเท่าไหร่ครับ???
กำหนดให้
(1) AB = AC
(2) BC = AD + BD
เป็นโจทย์เก่าของคุณ TIYHz ตั้งแต่ 22 มิถุนายน 2556
http://ppantip.com/topic/30636714
มีผู้เฉลยด้วยวิธีทางตรีโกณมิติไปแล้ว
ผมขอเสนอวิธีทั้งทางตรีโกณฯ และทางเรขาคณิต
วิธีทางเรขาฯ ของผมยาวมาก ผมอยากเห็นเพื่อนสมาชิกหรือผู้สนใจท่านอื่น ๆ เสนอวิธีที่กะทัดรัดกว่านี้
เพิ่มเติมวันที่ 19 กค 2556 ถ้าใครงง ๆ หรือขี้เกียจอ่านวิธีที่แสนจะสับสนของผม ให้ข้ามไปที่ คห 11 ดูเฉลยของคุณ TIYHz ได้เลย