วันนี้นั่งเล่นเฟสแล้วไปเจอภาพนี้เข้าจาก
P.Ach's scrap blog

ในตอนแรกผมก็เห็นด้วยกับรูปนั้น เพราะว่าไอพ่นชี้ไปด้านหลังเพียงอย่างเดียว ไม่ได้มีแรงยกตัวดังนั้นไม่มีทางบินได้แน่นอน
แต่พอไปนั่งอ่านคอมเม้นในนั้นก็พบว่ามีแนวคิดที่เป็นไปได้อยู่ โดยบอกว่า ironman เวลาบินจะแอ่นอกขึ้นเล็กน้อย
ทำให้ลมที่มาปะทะก่อให้เกิดแรงยกตัวให้ตัว ironman สามารถบินได้ขึ้นมา
พออ่านคอมเม้นนั้นก็เลยทำให้ผมสงสัยว่าแรงยกตัวแค่นั้นจะสามารถยก ironman ให้บินได้จริงเร้อ ก็เลยมาลองนั่งคำนวณเล่นดู
ปล.บอกไว้ก่อนว่าผมไม่ได้เรียนด้านอากาศพลศาสตร์มาโดยตรงนะครับ การคำนวณนี้เป็นเพียงการคำนวณแบบประมาณคร่าว ๆ เท่านั้น อาจจะคลาดเคลื่อนไปจากความเป็นจริงได้(มาก)
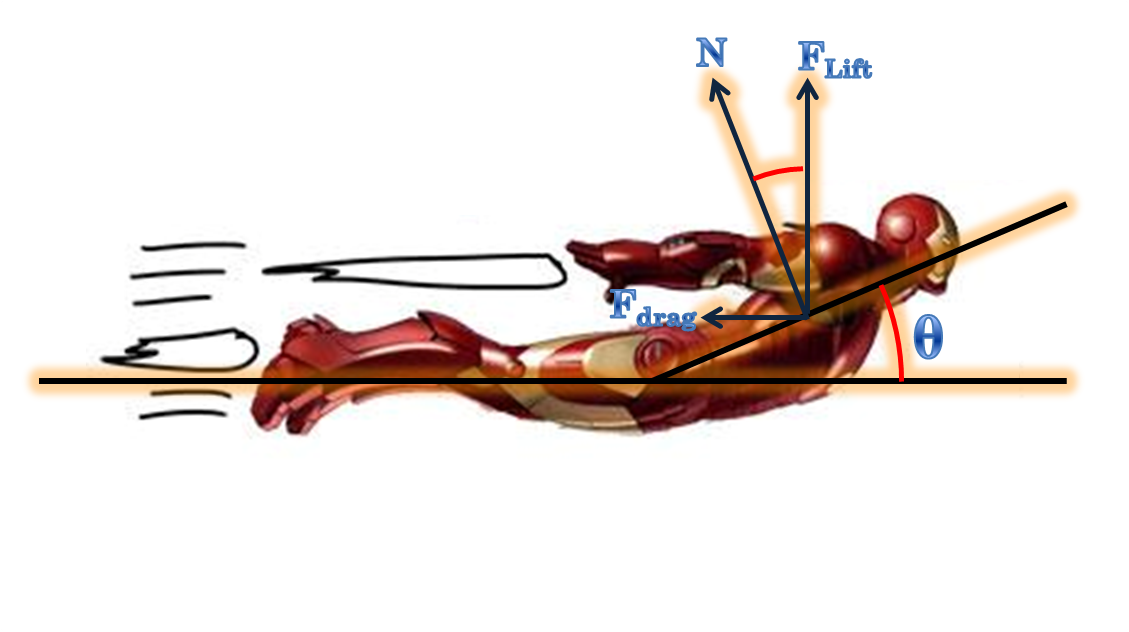
จากรูปจะเห็นได้ว่าแรงที่อากาศกระทำกับตัว ironman จะตั้งฉากกับตัวไอรอนแมน โดยสามารถแตกแรงออกมาได้เป็นแรงยก (F
Lift) และแรงต้าน (F
drag) ได้ ดังนั้นเมื่อเราหาแรงต้านที่กระทำต่อตัว ironman ได้ เราก็สามารถหาแรงยกได้ทันที
ในการหาแรงต้านอากาศนั้น สูตรที่ใช้คือ
[1]
F
drag = 1/2 ρv
2AC
d
โดยที่ ρ คือความหนาแน่นของอากาศขณะนั้น
v คือความเร็วของร่างกายเทียบกับอากาศ
A คือพื้นที่หน้าตัดของร่างกายที่ปะทะลม
C
d คือสัมประสิทธิ์ความต้านอากาศ
C
d ค่าสัมประสิทธิ์ความต้านอากาศสำหรับร่างกายมนุษย์นั้นจะอยู่ระหว่าง 0.35 ถึง 1.36 โดยขึ้นกับเสื้อผ้าและท่าทางในการฝ่าอากาศ
ในที่นี้ขอประมาณอยู่ที่ 0.50 เนื่องจากเอาหัวฝ่าอากาศโดยตรงและชุด ironman เป็นโลหะผิวเรียบลื่น
A พื้นที่หน้าตัด ในที่นี้จะคำนวนโดยคิดแค่เอวขึ้นมา โดยกำหนดให้เอวมีรูปร่างเป็นสี่เหลี่ยมผืนผ้า และหัวเป็นรูปวงรี
สมมติให้ไหล่กว้าง 40 เซนติเมตร และจากเอวขึ้นมาถึงคอสูง 45 เซนติเมตร จะมีพื้นที่หน้าตัด = 40*45 = 1800 cm
2
ให้ส่วนหัวยาว 23 เซนติเมตรและสูง 15 เซนติเมตร จะมีพื้นที่หน้าตัดวงรี = pi*a*b = 3.14*11.5*7.5 ≈ 270 cm
2
พื้นที่รวมเท่ากับ 1800+270 = 2070 cm
2 = 0.207 m
2
สมมติให้ ironman แอ่นหลังประมาณ 30 องศา
จะได้พื้นที่หน้าตัดที่ปะทะลม A = 0.207 * sin(30) ≈ 0.1 m
2
v ความเร็วของอากาศที่ปะทะ
Iron Man's Mark VI Suit สามารถบินได้ที่ความเร็วสูงสุด mach 1.2
[2]
ดังนั้นสมมติให้มีความเร็ว mach 1 หรือประมาณ 340 m/s
ρ ความหนาแน่นของอากาศ
ถ้าหาก ironman บินอยู่ที่ความสูง 5 กิโลเมตรจากระดับน้ำทะเล
อากาศจะมีความหนาแน่นราว ๆ 0.65 kg/m
3
ดังนั้น
F
drag = 1/2*0.65*340
2*0.1*0.5 = 1,878 N
และจากตรีโกณมิติจะได้ว่า
F
Lift = F
drag/tan 30
o
≈ 3,253 N
ถ้าหากให้ชุด ironman มีมวล 110 kg และสตาร์กมีมวล 70kg จะพบว่าน้ำหนักทั้งหมดรวมกันมีเพียง 180kg หรือ 1800 N เท่านั้น
ดังนั้นจึงสามารถเป็นไปได้ที่ ironman จะสามารถบินในท่านี้ได้
สำหรับความเร็วต่ำสุดที่จะทำให้ ironman สามารถบินได้นั้น สามารถคำนวณย้อนกลับได้โดย
mg = F
Lift = F
drag/tan 30
o
= 1/2 ρv
2AC
d/tan 30
o
v = sqrt[ 2mg tan(30)/{ρAC
d} ]
≈ 252m/s ≈ 907 km/hr
สรุปว่าจากการคำนวณแบบคร่าว ๆ (หรือพูดอีกอย่างก็คือมั่วนั่นแหละ) ของผมสามารถได้ข้อสรุปออกมาก็คือ ironman สามารถบินในท่านี้ได้จริงนั่นเอง
เป็นอันว่าสมมติฐานแรกสุดที่ผมตั้งไว้เป็นอันล้มครืน เพราะตอนแรกผมคิดว่าไม่มีทางบินได้ในท่านั้นอย่างแน่นอน
และที่มานั่งคำนวณก็เพื่อยืนยันความคิดของตัวเอง แต่สุดท้ายผลที่ออกมาดันตรงกันข้ามซะได้ 5555
[1]
Kinemetics of Human Motion: by Vladimir M. Zatsiorsky
[2]
http://www.marveldirectory.com/miscellaneous/ironmanmarkvi.htm
edit : แก้ไขตามคห.9
ท่าบินที่ถูกต้องของ Iron man.. จริงเหรอ...
ในตอนแรกผมก็เห็นด้วยกับรูปนั้น เพราะว่าไอพ่นชี้ไปด้านหลังเพียงอย่างเดียว ไม่ได้มีแรงยกตัวดังนั้นไม่มีทางบินได้แน่นอน
แต่พอไปนั่งอ่านคอมเม้นในนั้นก็พบว่ามีแนวคิดที่เป็นไปได้อยู่ โดยบอกว่า ironman เวลาบินจะแอ่นอกขึ้นเล็กน้อย
ทำให้ลมที่มาปะทะก่อให้เกิดแรงยกตัวให้ตัว ironman สามารถบินได้ขึ้นมา
พออ่านคอมเม้นนั้นก็เลยทำให้ผมสงสัยว่าแรงยกตัวแค่นั้นจะสามารถยก ironman ให้บินได้จริงเร้อ ก็เลยมาลองนั่งคำนวณเล่นดู
ปล.บอกไว้ก่อนว่าผมไม่ได้เรียนด้านอากาศพลศาสตร์มาโดยตรงนะครับ การคำนวณนี้เป็นเพียงการคำนวณแบบประมาณคร่าว ๆ เท่านั้น อาจจะคลาดเคลื่อนไปจากความเป็นจริงได้(มาก)
จากรูปจะเห็นได้ว่าแรงที่อากาศกระทำกับตัว ironman จะตั้งฉากกับตัวไอรอนแมน โดยสามารถแตกแรงออกมาได้เป็นแรงยก (FLift) และแรงต้าน (Fdrag) ได้ ดังนั้นเมื่อเราหาแรงต้านที่กระทำต่อตัว ironman ได้ เราก็สามารถหาแรงยกได้ทันที
ในการหาแรงต้านอากาศนั้น สูตรที่ใช้คือ[1]
Fdrag = 1/2 ρv2ACd
โดยที่ ρ คือความหนาแน่นของอากาศขณะนั้น
v คือความเร็วของร่างกายเทียบกับอากาศ
A คือพื้นที่หน้าตัดของร่างกายที่ปะทะลม
Cd คือสัมประสิทธิ์ความต้านอากาศ
Cd ค่าสัมประสิทธิ์ความต้านอากาศสำหรับร่างกายมนุษย์นั้นจะอยู่ระหว่าง 0.35 ถึง 1.36 โดยขึ้นกับเสื้อผ้าและท่าทางในการฝ่าอากาศ
ในที่นี้ขอประมาณอยู่ที่ 0.50 เนื่องจากเอาหัวฝ่าอากาศโดยตรงและชุด ironman เป็นโลหะผิวเรียบลื่น
A พื้นที่หน้าตัด ในที่นี้จะคำนวนโดยคิดแค่เอวขึ้นมา โดยกำหนดให้เอวมีรูปร่างเป็นสี่เหลี่ยมผืนผ้า และหัวเป็นรูปวงรี
สมมติให้ไหล่กว้าง 40 เซนติเมตร และจากเอวขึ้นมาถึงคอสูง 45 เซนติเมตร จะมีพื้นที่หน้าตัด = 40*45 = 1800 cm2
ให้ส่วนหัวยาว 23 เซนติเมตรและสูง 15 เซนติเมตร จะมีพื้นที่หน้าตัดวงรี = pi*a*b = 3.14*11.5*7.5 ≈ 270 cm2
พื้นที่รวมเท่ากับ 1800+270 = 2070 cm2 = 0.207 m2
สมมติให้ ironman แอ่นหลังประมาณ 30 องศา
จะได้พื้นที่หน้าตัดที่ปะทะลม A = 0.207 * sin(30) ≈ 0.1 m2
v ความเร็วของอากาศที่ปะทะ
Iron Man's Mark VI Suit สามารถบินได้ที่ความเร็วสูงสุด mach 1.2[2]
ดังนั้นสมมติให้มีความเร็ว mach 1 หรือประมาณ 340 m/s
ρ ความหนาแน่นของอากาศ
ถ้าหาก ironman บินอยู่ที่ความสูง 5 กิโลเมตรจากระดับน้ำทะเล
อากาศจะมีความหนาแน่นราว ๆ 0.65 kg/m3
ดังนั้น
Fdrag = 1/2*0.65*3402*0.1*0.5 = 1,878 N
และจากตรีโกณมิติจะได้ว่า
FLift = Fdrag/tan 30o
≈ 3,253 N
ถ้าหากให้ชุด ironman มีมวล 110 kg และสตาร์กมีมวล 70kg จะพบว่าน้ำหนักทั้งหมดรวมกันมีเพียง 180kg หรือ 1800 N เท่านั้น
ดังนั้นจึงสามารถเป็นไปได้ที่ ironman จะสามารถบินในท่านี้ได้
สำหรับความเร็วต่ำสุดที่จะทำให้ ironman สามารถบินได้นั้น สามารถคำนวณย้อนกลับได้โดย
mg = FLift = Fdrag/tan 30o
= 1/2 ρv2ACd/tan 30o
v = sqrt[ 2mg tan(30)/{ρACd} ]
≈ 252m/s ≈ 907 km/hr
สรุปว่าจากการคำนวณแบบคร่าว ๆ (หรือพูดอีกอย่างก็คือมั่วนั่นแหละ) ของผมสามารถได้ข้อสรุปออกมาก็คือ ironman สามารถบินในท่านี้ได้จริงนั่นเอง
เป็นอันว่าสมมติฐานแรกสุดที่ผมตั้งไว้เป็นอันล้มครืน เพราะตอนแรกผมคิดว่าไม่มีทางบินได้ในท่านั้นอย่างแน่นอน
และที่มานั่งคำนวณก็เพื่อยืนยันความคิดของตัวเอง แต่สุดท้ายผลที่ออกมาดันตรงกันข้ามซะได้ 5555
[1] Kinemetics of Human Motion: by Vladimir M. Zatsiorsky
[2] http://www.marveldirectory.com/miscellaneous/ironmanmarkvi.htm
edit : แก้ไขตามคห.9