หากลองนึกย้อนไปเมื่อเราอยู่ ป.1 ถ้ามีคนถามว่า จำนวนอะไรใหญ่ที่สุด เราก็คงตอบว่า 10 หรือไม่ก็ 20
ถ้าเราอยู่ซัก ป.6 แล้วมีคนถามเราว่า จำนวนอะไรใหญ่ที่สุด เราก็อาจจะตอบว่า ล้าน หรือ ล้าน ๆ หรือ ล้าน ๆๆๆๆๆๆๆๆๆๆๆๆๆ
เเต่เมื่อเราได้เรียนรู้มากขึ้นเรื่อย ๆ เราพบว่า จำนวนที่ใหญ่ที่สุด (จำนวนเต็ม) ไม่มี เพราะว่ามีจำนวนที่ใหญ่กว่าอยู่เสมอ เช่น ล้าน ๆๆๆๆๆๆๆๆๆๆๆๆๆ + 1

เพื่อให้ระบบจำนวนของเราสมบูรณ์ การไม่มีจำนวนที่มากที่สุดนั้นเป็นสิ่งที่ควรจะเป็นอยู่แล้ว
แต่ว่า ในบรรดาจำนวนมากมาย ที่เราสามารถสร้างขึ้นมาได้ไม่จำกัด จำนวนที่มีขนาดใหญ่เกินกว่าที่เราจะจินตนาการ
อย่างเช่น ผมเคยถามนักเรียนว่า ลองสร้างจำนวนที่เราคิดว่าใหญ่สุด ๆ ดูซิ ก็มีคนตอบหลายคำตอบ เช่น ล้าน ๆๆๆๆๆๆๆๆ หรือ ล้านยกกำลังล้าน บางคนก็ ล้านยกกำลังล้าน ล้านครั้ง ฯลฯ จินตนาการของเด็กล่ะนะ
แต่จำนวนเหล่านั้น มีความหมายอะไรล่ะ นอกจากขนาดของมันก็ไม่มีอะไรพิเศษเลย

แต่มีจำนวนอยู่จำนวนหนึ่ง ที่มีขนาดใหญ่โต และมีการใช้จริงในการพิสูจน์ทางคณิตศาสตร์ด้วย
ความสุดยอดของมันคือ มันใหญ่มาก ๆ เกินกว่าที่เราจะจินตนาการได้เลยทีเดียว
ขอแนะนำให้รู้จักกับ จำนวนของเกรแฮม (Graham's Number : g64)

Arrow Notation
ก่อนอื่น เราต้องทำความเข้าใจกับตัวดำเนินการอย่างหนึ่งก่อน คือ Arrow Notation บางคนก็เรียกว่า Knut's Up-Arrow notation
ขอเริ่มต้นด้วยหนึ่งหัวลูกศร(ขอยกตัวอย่างเลข 3 เพื่อความง่าย)
3↑3  = 3³ = 27
มันก็เป็นวิธีเขียน 3³ วิธีหนึ่งนั่นเอง หรืออีกตัวอย่าง เช่น  2↑3 = 2³ หรือ 12↑7 = 12⁷ เป็นต้น
ทีนี้ ถ้าลูกศรอันเดียวนั้นมันยังไม่น่าสนใจ เราลองเพิ่มลูกศรลงไปอีกหนึ่งอัน(จากนี้จะเริ่มแทรกรูปภาพลงไป เพราะเริ่มพิมพ์ยาก)
ถ้าให้ n เป็นจำนวนเต็มใด ๆ แล้ว 3↑↑n จะมีความหมายดังนี้



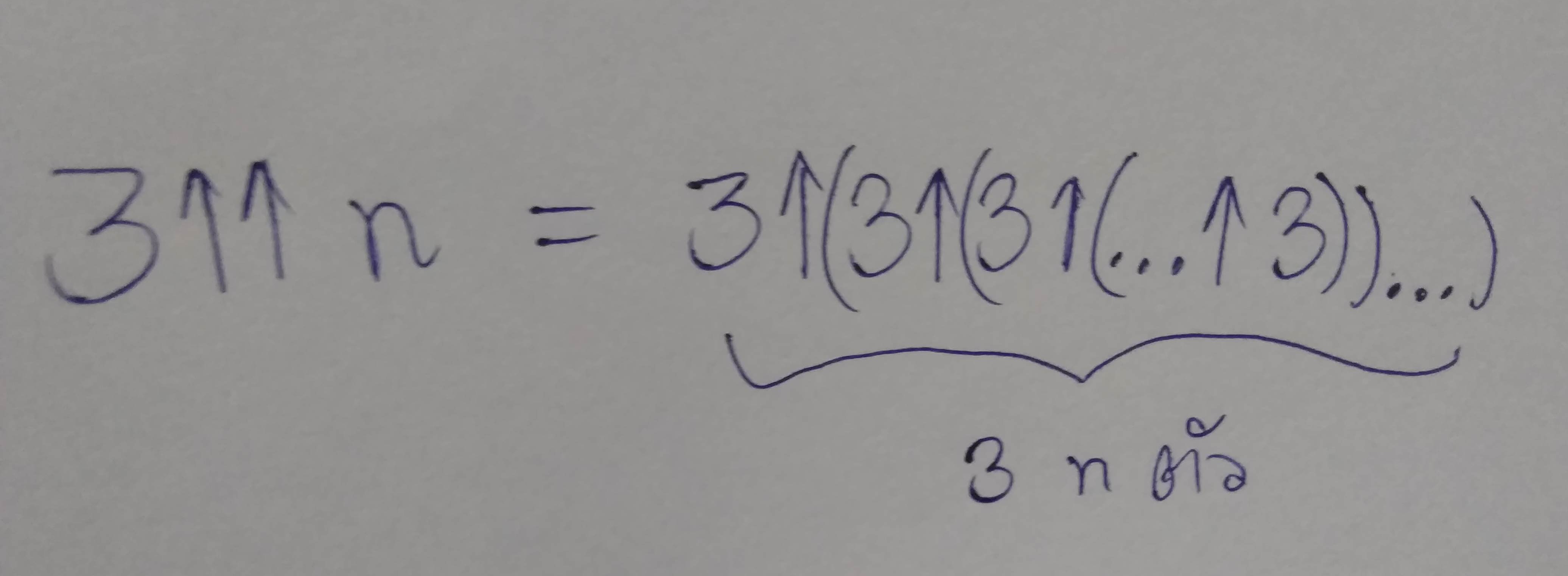
เช่น



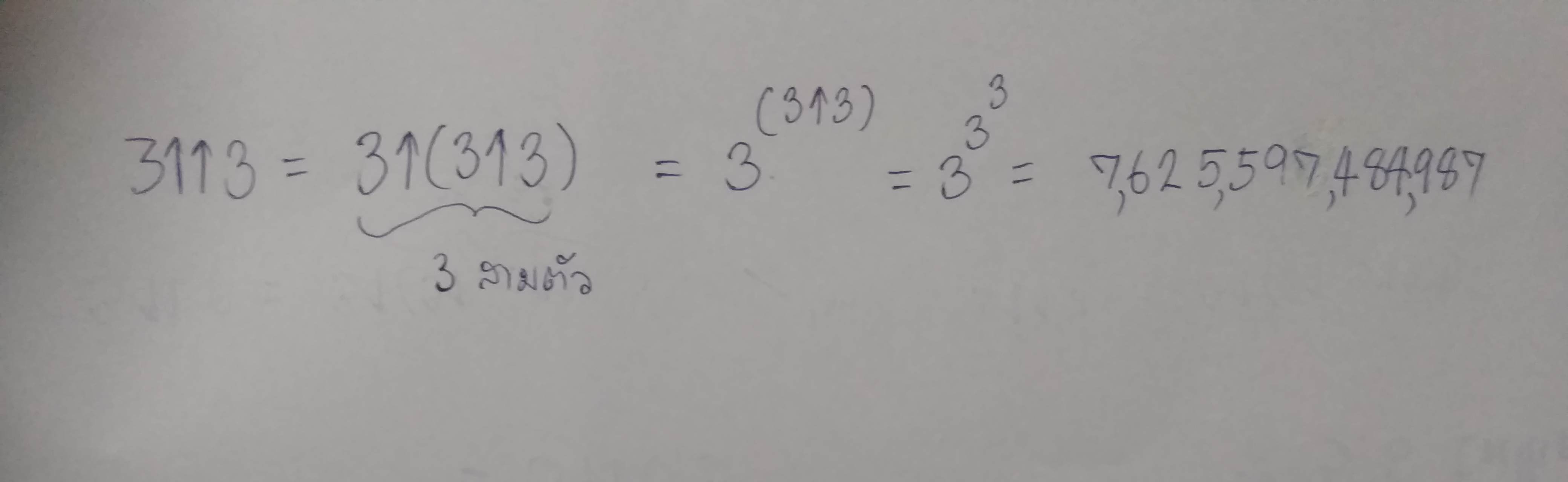
เราสังเกตอะไรกันมั้ยครับ
3↑3 = 3^3 = 27
แต่
3↑↑3 = 3^(3^3) = 7,625,597,484,987
เพียงแค่เพิ่มลูกศรขึ้นมา 1 อันเท่านั้น... ค่าของมันเพิ่มขึ้น อย่างมากเลยใช่มั้ยครับ
ทีนี้เราน่าจะมีความคิดเหมือนกัน คือ ถ้าเป็นลูกศร 3 อันล่ะ... จะเป็นอย่างไร
ก่อนอื่น 3↑↑↑3 ก็ไม่ต่างจาก 3↑↑3 มากนัก ดังนี้



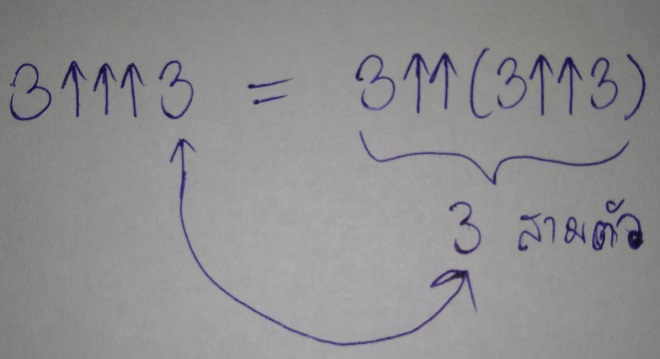
ซึ่งก็ไม่ได้เยอะเท่าไหร่ คำนวณได้ดังนี้



ที่บอกว่าไม่เยอะเท่าไหร่นั้นผมประชดนะครับ 555 ความจริงจำนวนนี้ใหญ่สุด ๆ ... ประมาณ 3.6 ล้านล้านหลัก

Graham's Number
ถ้าถามว่า เราเข้าใกล้จำนวนของเกรแฮมรึยัง บอกได้เลยว่า 3↑↑↑3 ยังมีขนาดไม่ถึงเศษเสี้ยวหนึ่งของจำนวนนี้ด้วยซ้ำ 
ก่อนจะไปถึงตรงนั้น เรามาเพิ่มลุกศรไปอีก 1 อันดีกว่า แล้วมาดูผลลัพธ์ว่าจะเป็นอย่างไร



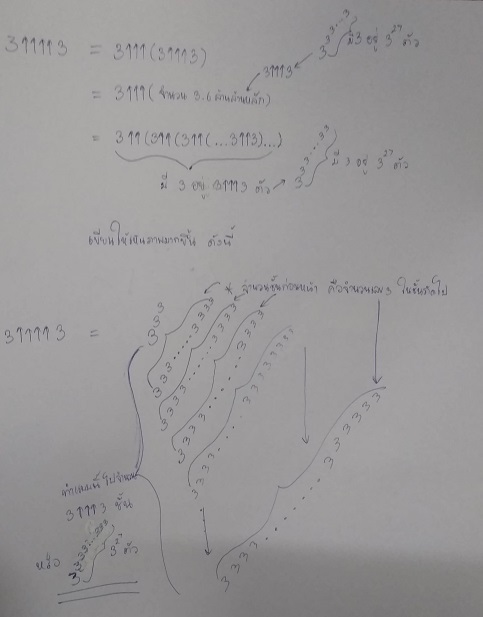
3↑↑↑3 ก็ว่าใหญ่แล้ว แต่เทียบกับ 3↑↑↑↑3 ไม่ติดเลยใช่มั้ยล่ะครับ
เราเรียก 

 3↑↑↑↑3

ว่า g₁
ส่วน g₂ คือจำนวนที่มีลูกศรอยู่ระหว่างเลข 3 จำนวน g₁ ตัว ... ตอนนี้จำนวนของเรา ใหญ่เกินคำบรรยายไปแล้วครับ
และ g₃ ก็มีจำนวนลูกศรอยู่ระหว่างเลข 3 จำนวน g₂ ตัว ... ซึ่งก็เขียนให้เห็นภาพได้ดังนี้



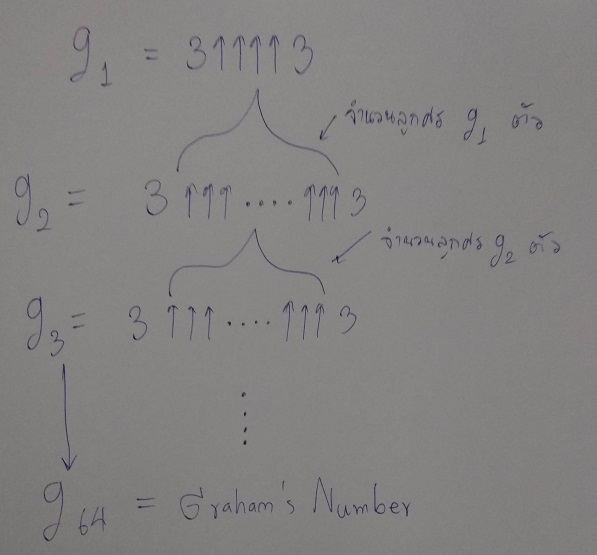
ตามภาพเลยครับ Graham's Number มีค่าเท่ากับ g₆₄ นั่นก็คือต้องทำแบบนั้นไปถึง 64 ชั้น จึงจะได้ Graham's Number
เป้นจำนวนที่มีขนาดที่ใหญ่ที่สุด เท่าที่เคยมีการใช้ในการพิสูจน์ทางคณิตศาสตร์ ตามบันทึกของ Guinness Book

 Graham's Number สร้างขึ้นโดยนักคณิตศาสตร์ชื่อ Ron Graham ซึ่งปัจจุบันยังมีชีวิตอยู่ โดยเป็นขอบเขตบน ของปัญหาที่ชื่อว่า Ramsey Theory 

ซึ่งปัจจุบันก็มีคนที่หาขอบเขตบนที่ดีกว่าสำหรับปัญหานี้ได้แล้ว แต่ทุก ๆ การค้นพบก็จำเป็นต้องมีการเริ่มต้น เเละมีการพัฒนาต่อยอดไปสู่ผลลัพธ์ที่ดีขึ้น ก็นับได้ว่า Ron Graham นั้นเริ่มต้นได้ค่อนข้างน่าตื่นตาตื่นใจ กับ Graham's Number ของเขา ที่ได้สร้างสีสันและความน่าสนใจ เกี่ยวกับวิชาคณิตศาสตร์ที่น่าเบื่อ ให้น่าตื่นเต้นมากขึ้น ด้วยความสุดยอดในเรื่องขนาดของมัน

เอกภพกว้างใหญ่ ธรรมชาตินั้นน่าค้นหา เพียงแค่เราไม่หยุดค้นคว้า เราก็จะพบความหมายของชีวิตที่เราตามหา ในท้ายที่สุดของการเดินทาง

[Spoil] คลิกเพื่อดูข้อความที่ซ่อนไว้ขอบคุณที่อ่านจนจบนะครับ ถ้ามีความคิดเห็นอย่างไร ก็สามารถทิ้งคอมเมนต์เอาไว้ได้นะครับ หรือมีความรู้อะไรเพิ่มเติมจากที่ผมได้เขียนมา ก็สามารถนำมาแบ่งปันกันได้นะครับ ผมจะดีใจมาก ๆ เลยครับ