คำตอบที่ได้รับเลือกจากเจ้าของกระทู้
ความคิดเห็นที่ 23
ใครที่สงสัยเรื่องการเดินทางใกล้ความเร็วแสงแล้วเวลาช้าลง ผมเคยเขียนเรื่องการยืดออกของเวลาไว้นิดนึงครับ ลองอ่านดูครับเผื่อจะช่วยได้
ก่อนอื่นมาทำความรู้จักสัจพนน์ของไอน์สไตน์กันก่อนครับ
สัจพจน์ข้อที่ 1 ของไอน์สไตน์ ในกรอบอ้างอิงเฉื่อยทุกกรอบ กฎเกณฑ์หรือสมการทางฟิสิกส์จะมีรูปเดียวกันเสมอ
สัจพจน์ข้อที่ 2 ของไอน์สไตน์ อัตราเร็วของแสงในสุญญากาศมีค่าคงที่ 3x108m/s ไม่ขึ้นกับการเคลื่อนที่ของแหล่งกำเนิดแสงหรือผู้สังเกต
มาพูดถึงการยืดออกของเวลา(Time Dilation) กันเลยครับ
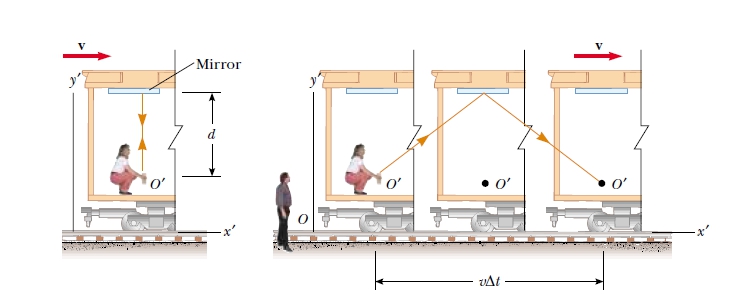 ผมจะยกตัวอย่างเหตุการณ์หนึ่งขึ้นมา เป็นเหตุการณ์ที่มีผู้หญิงคนหนึ่งนั่งอยู่ในรถไฟที่วิ่งอยู่ ทำการฉายไฟฉายขึ้นไปบนเพดานซึ่งมีประจกเงาอยู่ด้านบนและสะท้อนกลับลงมา และมีผู้ชายอีกคนเป็นผู้สังเกตที่อยู่นิ่งอยู่นอกรถไฟ โดยที่เหตุการณ์นี้เกิดขึ้นพร้อมกัน
ผมจะยกตัวอย่างเหตุการณ์หนึ่งขึ้นมา เป็นเหตุการณ์ที่มีผู้หญิงคนหนึ่งนั่งอยู่ในรถไฟที่วิ่งอยู่ ทำการฉายไฟฉายขึ้นไปบนเพดานซึ่งมีประจกเงาอยู่ด้านบนและสะท้อนกลับลงมา และมีผู้ชายอีกคนเป็นผู้สังเกตที่อยู่นิ่งอยู่นอกรถไฟ โดยที่เหตุการณ์นี้เกิดขึ้นพร้อมกัน
ผู้สังเกตคนที่ 1 (ผู้หญิง)
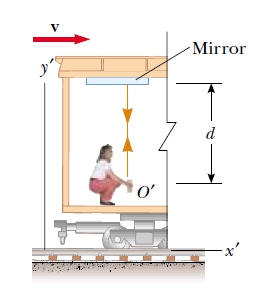 ผู้สังเกตที่นี้จะเห็นแสงเดินทางขึ้นไปจากไฟฉาย และสะท้อนกลับลงมาที่กระบอกไฟฉายในเส้นทางเดียวกัน
ผู้สังเกตที่นี้จะเห็นแสงเดินทางขึ้นไปจากไฟฉาย และสะท้อนกลับลงมาที่กระบอกไฟฉายในเส้นทางเดียวกัน
โดยเวลาที่ผู้สังเกตที่ 1 เห็นแสงเดินทางตั้งแต่ต้นจนจบเป็นตามสมการ
 สมการที่ 1
สมการที่ 1
โดยให้ △tp เป็นเวลาของเหตุการณ์ที่สังเกตโดยผู้สังเกตที่ 1
ผู้สังเกตคนที่ 2(ผู้ชาย)
 จากผู้สังเกตที่ 1 ได้ทำการฉายไฟจากกระบอกไฟฉายที่ฉายอยู่ในมือ ขึ้นไปที่กระจกด้านบนและสะท้อนลงมาที่ไฟฉายของเขา ผู้สังเกตคนที่ 2 ก็ต้องเห็นเหตุการณ์เป็นเหตุการณ์แบบเดียวกับผู้สังเกตที่ 1 ครับ แต่เนื่องจากตอนนี้ ผู้สังเกตที่ 1 นั้นนั่งอยู่ในรถไฟซึ่งมีความเร็ว นั่นหมายความว่าผู้สังเกตคนที่ 2 จะเห็นจุดที่แสงออกจากกระบอกไฟฉาย จุดที่แสงกระทบกระจกและกำลังจะสะท้อน และจุดที่แสงสะท้อนลงมาถึงไฟฉายอีกครั้ง นั้นเป็นจุดที่ต่างกัน และการที่จุดแต่ละจุดต่างกัน
จากผู้สังเกตที่ 1 ได้ทำการฉายไฟจากกระบอกไฟฉายที่ฉายอยู่ในมือ ขึ้นไปที่กระจกด้านบนและสะท้อนลงมาที่ไฟฉายของเขา ผู้สังเกตคนที่ 2 ก็ต้องเห็นเหตุการณ์เป็นเหตุการณ์แบบเดียวกับผู้สังเกตที่ 1 ครับ แต่เนื่องจากตอนนี้ ผู้สังเกตที่ 1 นั้นนั่งอยู่ในรถไฟซึ่งมีความเร็ว นั่นหมายความว่าผู้สังเกตคนที่ 2 จะเห็นจุดที่แสงออกจากกระบอกไฟฉาย จุดที่แสงกระทบกระจกและกำลังจะสะท้อน และจุดที่แสงสะท้อนลงมาถึงไฟฉายอีกครั้ง นั้นเป็นจุดที่ต่างกัน และการที่จุดแต่ละจุดต่างกัน
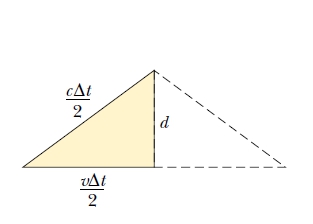 รูปนี้จะเป็นระยะที่ผู้สังเกตที่ 2 เห็นแสงเดินทางครับ โดยให้ △t เป็นเวลาของเหตุการณ์ที่สังเกตโดยผู้สังเกตที่ 2 จากทฤษฎีบทพีทาโกรัสจะได้ว่า
รูปนี้จะเป็นระยะที่ผู้สังเกตที่ 2 เห็นแสงเดินทางครับ โดยให้ △t เป็นเวลาของเหตุการณ์ที่สังเกตโดยผู้สังเกตที่ 2 จากทฤษฎีบทพีทาโกรัสจะได้ว่า
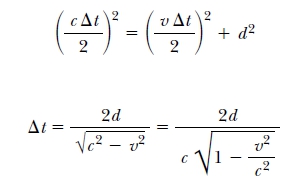 สมการที่ 2
สมการที่ 2
จากสมการที่ 1 นำมาแทนในสมการที 2 จะได้ว่า
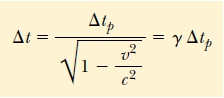 สมการที่ 3
สมการที่ 3
นี่เป็นความสัมพันธ์ระหว่าง △tp กับ △t
โดย △tp จะเป็นช่วงเวลาของเหตุการณ์ของผู้สังเกตที่เห็นเหตุการณ์เกิดขึ้นที่จุดเดียวกัน (ในที่นี้คือผู้หญิงที่นั่งในรถไฟ)
△t จะเป็นช่วงเวลาของเหตุการณ์ของผู้สังเกตการณ์ที่เห็นเหตุการณ์เกิดขึ้นคนละจุดกัน (ในที่นี้คือผู้ชายที่ยืนอยู่ด้านนอก)
เรามาดูกันครับว่า ถ้าเกิด v มีค่าใกล้เคียงความเร็วแสงจะเกิดอะไรขึ้น?
สมมติมีฝาแฝด 1 คู่ อายุ 20 ปี(สมมติเป็น B1 กับ B2) โดยที่ B1อยู่ที่โลก และB2เดินทางออกจากโลกไปยังดาวนาเมกด้วยความเร็ว 0.9c
B2 ทำการจับเวลาตั้งแต่ออกจากโลกจนกลับมาถึงโลก พบว่าใช้เวลาไป 10 ปี อยากรู้ว่าตอนนั้น B1 จะมีอายุเป็นเท่าไร
จากสมการที่ 3 ที่ผมอธิบายด้านบนยาวเหยียด เมื่อนำค่าไปแทน จะบนว่า △t จะมีค่าประมาณ 23 ปี
ก็คือเวลาของนาย B2 ผ่านไป 10 ปี แต่เวลาของนาย B1 ผ่านไปตั้ง 23 ปี
หมายความว่า อายุของทั้งคู่จะไม่เท่ากันเมื่อทั้งคู่กลับมาเจอกันอีกครั้ง โดยนาย B1 จะมีอายุ 20+23=43 ปี แต่นาย B2 จะมีอายุแค่ 30 ปี
โดยปรากฏการณ์ Time Dilation นี่จะเกิดขึ้นเมื่อความเร็วมีค่ามากๆ ยิ่งใกล้ความเร็วแสง ยิ่งเห็นผลมากครับ
ขอบคุณรูปปลากรอบจาก Physics for Scientists and Engineers 6th ed. - Serway and Jewett ครับ
ผิดพลาดประการใดขออภัยด้วยครับ
ก่อนอื่นมาทำความรู้จักสัจพนน์ของไอน์สไตน์กันก่อนครับ
สัจพจน์ข้อที่ 1 ของไอน์สไตน์ ในกรอบอ้างอิงเฉื่อยทุกกรอบ กฎเกณฑ์หรือสมการทางฟิสิกส์จะมีรูปเดียวกันเสมอ
สัจพจน์ข้อที่ 2 ของไอน์สไตน์ อัตราเร็วของแสงในสุญญากาศมีค่าคงที่ 3x108m/s ไม่ขึ้นกับการเคลื่อนที่ของแหล่งกำเนิดแสงหรือผู้สังเกต
มาพูดถึงการยืดออกของเวลา(Time Dilation) กันเลยครับ
 ผมจะยกตัวอย่างเหตุการณ์หนึ่งขึ้นมา เป็นเหตุการณ์ที่มีผู้หญิงคนหนึ่งนั่งอยู่ในรถไฟที่วิ่งอยู่ ทำการฉายไฟฉายขึ้นไปบนเพดานซึ่งมีประจกเงาอยู่ด้านบนและสะท้อนกลับลงมา และมีผู้ชายอีกคนเป็นผู้สังเกตที่อยู่นิ่งอยู่นอกรถไฟ โดยที่เหตุการณ์นี้เกิดขึ้นพร้อมกัน
ผมจะยกตัวอย่างเหตุการณ์หนึ่งขึ้นมา เป็นเหตุการณ์ที่มีผู้หญิงคนหนึ่งนั่งอยู่ในรถไฟที่วิ่งอยู่ ทำการฉายไฟฉายขึ้นไปบนเพดานซึ่งมีประจกเงาอยู่ด้านบนและสะท้อนกลับลงมา และมีผู้ชายอีกคนเป็นผู้สังเกตที่อยู่นิ่งอยู่นอกรถไฟ โดยที่เหตุการณ์นี้เกิดขึ้นพร้อมกัน ผู้สังเกตคนที่ 1 (ผู้หญิง)
 ผู้สังเกตที่นี้จะเห็นแสงเดินทางขึ้นไปจากไฟฉาย และสะท้อนกลับลงมาที่กระบอกไฟฉายในเส้นทางเดียวกัน
ผู้สังเกตที่นี้จะเห็นแสงเดินทางขึ้นไปจากไฟฉาย และสะท้อนกลับลงมาที่กระบอกไฟฉายในเส้นทางเดียวกันโดยเวลาที่ผู้สังเกตที่ 1 เห็นแสงเดินทางตั้งแต่ต้นจนจบเป็นตามสมการ
 สมการที่ 1
สมการที่ 1โดยให้ △tp เป็นเวลาของเหตุการณ์ที่สังเกตโดยผู้สังเกตที่ 1
ผู้สังเกตคนที่ 2(ผู้ชาย)
 จากผู้สังเกตที่ 1 ได้ทำการฉายไฟจากกระบอกไฟฉายที่ฉายอยู่ในมือ ขึ้นไปที่กระจกด้านบนและสะท้อนลงมาที่ไฟฉายของเขา ผู้สังเกตคนที่ 2 ก็ต้องเห็นเหตุการณ์เป็นเหตุการณ์แบบเดียวกับผู้สังเกตที่ 1 ครับ แต่เนื่องจากตอนนี้ ผู้สังเกตที่ 1 นั้นนั่งอยู่ในรถไฟซึ่งมีความเร็ว นั่นหมายความว่าผู้สังเกตคนที่ 2 จะเห็นจุดที่แสงออกจากกระบอกไฟฉาย จุดที่แสงกระทบกระจกและกำลังจะสะท้อน และจุดที่แสงสะท้อนลงมาถึงไฟฉายอีกครั้ง นั้นเป็นจุดที่ต่างกัน และการที่จุดแต่ละจุดต่างกัน
จากผู้สังเกตที่ 1 ได้ทำการฉายไฟจากกระบอกไฟฉายที่ฉายอยู่ในมือ ขึ้นไปที่กระจกด้านบนและสะท้อนลงมาที่ไฟฉายของเขา ผู้สังเกตคนที่ 2 ก็ต้องเห็นเหตุการณ์เป็นเหตุการณ์แบบเดียวกับผู้สังเกตที่ 1 ครับ แต่เนื่องจากตอนนี้ ผู้สังเกตที่ 1 นั้นนั่งอยู่ในรถไฟซึ่งมีความเร็ว นั่นหมายความว่าผู้สังเกตคนที่ 2 จะเห็นจุดที่แสงออกจากกระบอกไฟฉาย จุดที่แสงกระทบกระจกและกำลังจะสะท้อน และจุดที่แสงสะท้อนลงมาถึงไฟฉายอีกครั้ง นั้นเป็นจุดที่ต่างกัน และการที่จุดแต่ละจุดต่างกัน รูปนี้จะเป็นระยะที่ผู้สังเกตที่ 2 เห็นแสงเดินทางครับ โดยให้ △t เป็นเวลาของเหตุการณ์ที่สังเกตโดยผู้สังเกตที่ 2 จากทฤษฎีบทพีทาโกรัสจะได้ว่า
รูปนี้จะเป็นระยะที่ผู้สังเกตที่ 2 เห็นแสงเดินทางครับ โดยให้ △t เป็นเวลาของเหตุการณ์ที่สังเกตโดยผู้สังเกตที่ 2 จากทฤษฎีบทพีทาโกรัสจะได้ว่า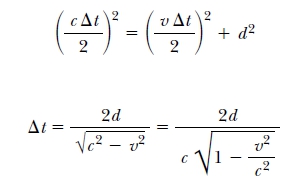 สมการที่ 2
สมการที่ 2จากสมการที่ 1 นำมาแทนในสมการที 2 จะได้ว่า
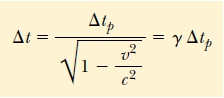 สมการที่ 3
สมการที่ 3นี่เป็นความสัมพันธ์ระหว่าง △tp กับ △t
โดย △tp จะเป็นช่วงเวลาของเหตุการณ์ของผู้สังเกตที่เห็นเหตุการณ์เกิดขึ้นที่จุดเดียวกัน (ในที่นี้คือผู้หญิงที่นั่งในรถไฟ)
△t จะเป็นช่วงเวลาของเหตุการณ์ของผู้สังเกตการณ์ที่เห็นเหตุการณ์เกิดขึ้นคนละจุดกัน (ในที่นี้คือผู้ชายที่ยืนอยู่ด้านนอก)
เรามาดูกันครับว่า ถ้าเกิด v มีค่าใกล้เคียงความเร็วแสงจะเกิดอะไรขึ้น?
สมมติมีฝาแฝด 1 คู่ อายุ 20 ปี(สมมติเป็น B1 กับ B2) โดยที่ B1อยู่ที่โลก และB2เดินทางออกจากโลกไปยังดาวนาเมกด้วยความเร็ว 0.9c
B2 ทำการจับเวลาตั้งแต่ออกจากโลกจนกลับมาถึงโลก พบว่าใช้เวลาไป 10 ปี อยากรู้ว่าตอนนั้น B1 จะมีอายุเป็นเท่าไร
จากสมการที่ 3 ที่ผมอธิบายด้านบนยาวเหยียด เมื่อนำค่าไปแทน จะบนว่า △t จะมีค่าประมาณ 23 ปี
ก็คือเวลาของนาย B2 ผ่านไป 10 ปี แต่เวลาของนาย B1 ผ่านไปตั้ง 23 ปี
หมายความว่า อายุของทั้งคู่จะไม่เท่ากันเมื่อทั้งคู่กลับมาเจอกันอีกครั้ง โดยนาย B1 จะมีอายุ 20+23=43 ปี แต่นาย B2 จะมีอายุแค่ 30 ปี
โดยปรากฏการณ์ Time Dilation นี่จะเกิดขึ้นเมื่อความเร็วมีค่ามากๆ ยิ่งใกล้ความเร็วแสง ยิ่งเห็นผลมากครับ
ขอบคุณรูปปลากรอบจาก Physics for Scientists and Engineers 6th ed. - Serway and Jewett ครับ
ผิดพลาดประการใดขออภัยด้วยครับ
สุดยอดความคิดเห็น
แสดงความคิดเห็น



 5.5 ปี ที่ ความเร็ว 99%ของความเร็วเเสง
5.5 ปี ที่ ความเร็ว 99%ของความเร็วเเสง
ถ้าคนเราสร้างยานความเร็วแสงได้ และเดินทางไป TRAPPIST-1 หากใช้เวลา 40 ปีแสงจริง เวลาบนยานและคนบนยานจะเป็นอย่างไร
เรื่องระยะทางกับเวลาผมสมมติขึ้นมานะครับเพราะไม่รุ้ว่า เดินทางเร็วขนาดนั้นจริงๆแล้ว เวลาจะเหลื่อมล้ำกันจริงๆเท่าไหร่ ที่แน่ๆตามทฤษฎีไอสไตน์ บนยานกับบนโลกไม่เท่ากันแน่ๆ