1) ก่อนอื่นผมไม่แน่ใจว่าใครเป็นคนคิด matrix คนแรกนะครับ(เดิมทีมันมีปรากฎทั้งอยู่ในตำราโบราณของจีน ญี่ปุ่น ดัตช์ ฯลฯ) แต่นิยาม"ตัวมัน"มาจากความสวยงามของมันในการใช้แก้ระบบสมการเชิงเส้น นิยามการคูณ matrix ก็เกิดขึ้นมาต่อจากตรงนี้ ผมเคยอ่านในหนังสือพวก linear algebra เมื่อนานมาแล้ว เหตุผลที่เขานิยามให้มันเป็นแบบนี้ก็เพราะมันมีประโยชน์ครับ ถ้าเราอยากนิยามการคูณ matrix แบบอื่นก็ได้(เช่นเอาสมาชิกคูณกันตรงๆ) แต่มันไม่ได้ช่วยในการแก้ระบบสมการเชิงเส้น

อีกอย่างการคูณ matrix แบบที่เราใช้ๆกันอยู่ มันดู "natural" กว่า  
natural กว่ายังไง?
ยกตัวอย่าง ถ้าเรามีสมการ ax+by = c และสมการ mx+ny = d ด้วยนิยามการคูณของ matrix เราสามารถเขียนสองสมการนี้ในรูป
[ a b ; c d ][x ; y] = [c ; d] ได้เลยตรงๆ(เครื่องหมาย ; หมายถึงขั้นแถวต่อไป) ถ้าเป็นนิยามการคูณแบบอื่นคงทำแบบนี้ไม่ได้

อีกอย่างถ้าดูดีๆ การคูณ matrix มันเหมือนการเอา vector มาดอทกันด้วย ซึ่งเป็นอีกเหตุผลสำคัญเลย

2) ส่วนสิ่งที่น่าจะถือว่าเป็น generalization ของ matrix ในหลายๆมิติได้ก็คงเป็นเทนเซอร์(Tensor) ครับ
เช่นเจ้าตัวนี้ Levi-Civita tensor



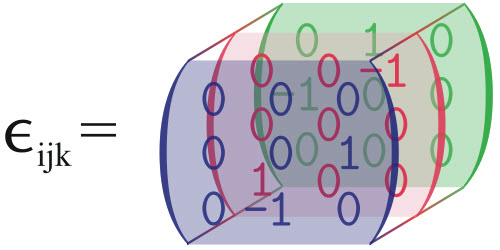
แก้ไข* ลืมตอบไปว่า tensor มันคูณกันยังไง
ตอบแบบคร่าวๆนะครับ ถ้าสนใจนิยามลองไปหาอ่านดู

การคูณของ tensor จะเป็นในลักษณ์เอาสมาชิกแต่ละตัวคูณกันแล้วจับมาบวกกัน(คุ้นๆไหม)

อย่างแรกเลยลองนึกถึง vector สองตัวดอทกันครับ vector ก็เป็น tensor แบบหนึ่งเรียกว่า First-rank tensor
ถ้าเรามีเวกเตอร์สองตัวเวลาดอทกัน เราก็เอาแต่ละ component มาคูณกันแล้วบวกกัน ได้ผลลัพธ์เป็นตัวเลขธรรมดา(สเกล่าร์)

หรือถ้าเรามี matrix ซึ่งก็เป็น tensor แบบหนึ่งเช่นกัน(เป็น Second-rank tensor) มาคูณกับ vector (First-rank tensor) สังเกตว่าเราจะได้ vector เช่นตัวอย่างเรื่องระบบสมการด้านบน ข้างซ้ายเป็น matrix คูณ vector ส่วนข้างขวาเป็น vector  
สังเกตว่าการคูณในกรณีนี้จะเอาแต่ละ component ของ vector มาคูณกับสมาชิกแต่ละแถวของ matrix แล้วบวกกัน ได้ผลลัพธ์เป็น component ใหม่ของ vector ตัวใหม่

หรือถ้าเรามี matrix สองตัวมาคูณกัน ผลลัพธ์ก็จะเป็น matrix  คราวนี้คล้ายๆกับการเอาเวกเตอร์ดอทกันเป็นคู่ๆหลายคู่ ได้ผลลัพธ์เป็น matrix ตัวใหม่

หรือถ้าสูงกว่านี้อีกอย่าง Third-rank tensor เราก็จะพบว่านิยามการคูณก็ไม่ต่างจากเดิมเท่าไหร่ เพียงแต่ว่าผลลัพธ์มันจะขึ้นอยู่กับว่าเราเอา tensor ที่มี rank ไหนคูณ rank ไหน อาจจะเป็นสเกล่าร์ เวกเตอร์ เมตริกซ์ หรือสูงกว่านั้นก็ได้