สุดยอดความคิดเห็น
ความคิดเห็นที่ 1
อื้อหือ มาเป็นคอมโบเลยแฮะ แต่ก็ดีแล้วละคับ จะได้เข้าใจว่าที่เค้าหยิบๆ มาใช้กันนี่มาได้ยังไง
เอาทีละอย่างละกันคับ จะทยอยลงเรื่อย
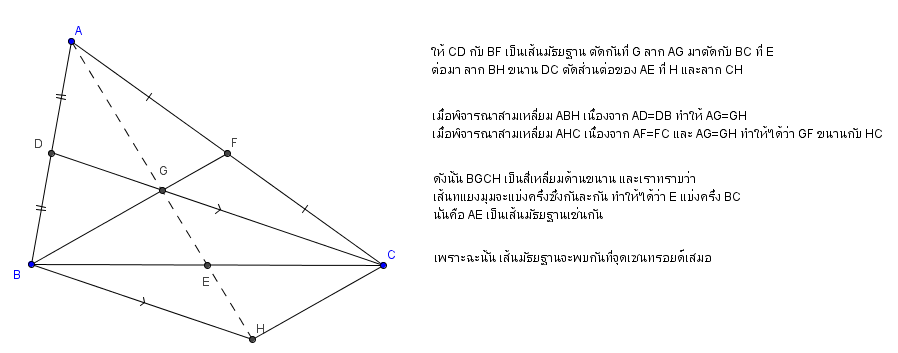
- ทำไมเส้นมัธยฐานถึงพบกันที่จุดเซนทรอยด์เสมอ
[Spoil] คลิกเพื่อดูข้อความที่ซ่อนไว้
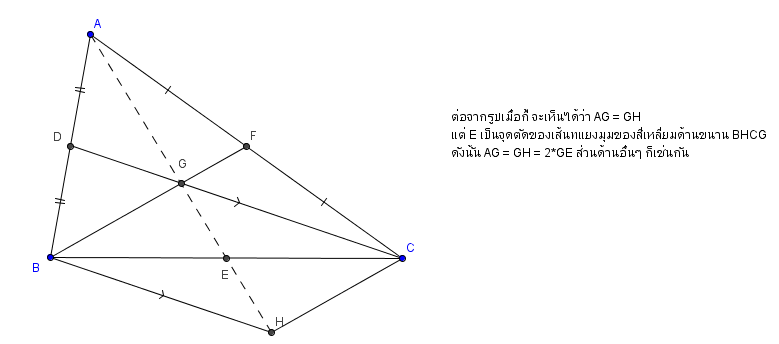
- ทำไมจุดเซนทรอยด์ถึงแบ่งเส้นมัธยฐานเป็นอัตราส่วน 2:1
[Spoil] คลิกเพื่อดูข้อความที่ซ่อนไว้
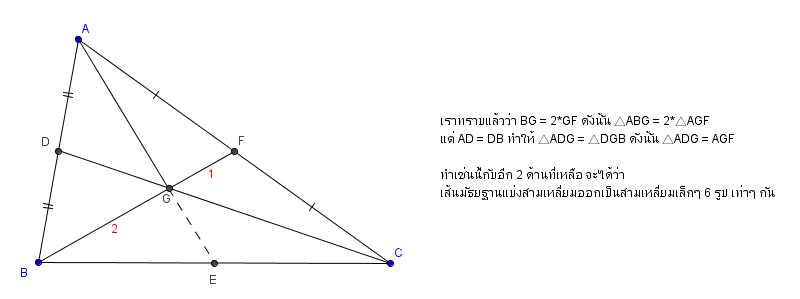
- ทำไมเส้นมัธยฐานถึงแบ่งสามเหลี่ยมออกเป็น 3 ส่วนเท่าๆ กัน
(จะพิสูจน์แรงกว่านี้ก็คือ แบ่งออกเป็น 6 ส่วนเล็กๆ เท่าๆ กัน)
[Spoil] คลิกเพื่อดูข้อความที่ซ่อนไว้
เอาทีละอย่างละกันคับ จะทยอยลงเรื่อย
- ทำไมเส้นมัธยฐานถึงพบกันที่จุดเซนทรอยด์เสมอ
[Spoil] คลิกเพื่อดูข้อความที่ซ่อนไว้
- ทำไมจุดเซนทรอยด์ถึงแบ่งเส้นมัธยฐานเป็นอัตราส่วน 2:1
[Spoil] คลิกเพื่อดูข้อความที่ซ่อนไว้
- ทำไมเส้นมัธยฐานถึงแบ่งสามเหลี่ยมออกเป็น 3 ส่วนเท่าๆ กัน
(จะพิสูจน์แรงกว่านี้ก็คือ แบ่งออกเป็น 6 ส่วนเล็กๆ เท่าๆ กัน)
[Spoil] คลิกเพื่อดูข้อความที่ซ่อนไว้
ความคิดเห็นที่ 2
ทำรูปมาฝาก

> ทำไมมันถึงแบ่งด้านนั้นๆ ด้วยความยาว-(หรืออัตราส่วนก็ไม่รู้)
>เท่ากับอัตราส่วนของพื้นที่ที่ไม่ติดกับเส้นนั้นๆ?
แปลงเป็นโจทย์ต้องการพิสูจน์ว่า
"พท.สามเหลี่ยมเขียว ACG: พท.สามเหลี่ยมเหลือง BCG= ด้านเขียว AF: ด้านเหลือง BF"

จากรูป
สามเหลี่ยมเขียวใหญ่ ACF กับ สามเหลี่ยมเหลืองใหญ่ BCF มีความสูงเท่ากัน
ดังนั้น
พท. สามเหลี่ยมเขียวใหญ่ ACF : พท.สามเหลี่ยมเหลืองใหญ่ BCF
= ด้านเขียว AF : ด้านเหลือง BF
ทำนองเดียวกัน
สามเหลี่ยมเขียวอ่อน AGF กับ สามเหลี่ยมเหลืองอ่อน BGF มีความสูงเท่ากัน
ดังนั้น
สามเหลี่ยมเขียวอ่อน AGF : สามเหลี่ยมเหลืองอ่อน BGF
= ด้านเขียว AF : ด้านเหลือง BF
แต่ พท.เขียว ACG = พท.เขียวใหญ่ ACF - พท.เขียวอ่อน AGF
และ พท.เหลือง BCG = พท.เหลืองใหญ่ BCF - พท.เหลืองอ่อน BGF
ดังนั้น
--------------------------------------------------------------------
พท.เขียว ACG : พท.เหลือง BCG = ด้านเขียว : ด้านเหลือง
--------------------------------------------------------------------
ส่วนคำถามเหล่านี้ ก็พิสูจน์ทำนองเดียวกัน
>แล้วทำไมเส้นที่เป็นด้านร่วมกันของสามเหลี่ยมย่อย 2 รูปในนั้น
>ถึงยาวเท่ากับขนาด(หรืออัตราส่วนก็ไม่รู้)ของพื้นที่นั้นบวกกัน?
>แล้วทำไมเส้นที่ลากต่อมาตัดด้านเมื่อกี้ ถึงยาวเท่ากับอัตราส่วนของพื้นที่ที่มันลากผ่าน?

> ทำไมมันถึงแบ่งด้านนั้นๆ ด้วยความยาว-(หรืออัตราส่วนก็ไม่รู้)
>เท่ากับอัตราส่วนของพื้นที่ที่ไม่ติดกับเส้นนั้นๆ?
แปลงเป็นโจทย์ต้องการพิสูจน์ว่า
"พท.สามเหลี่ยมเขียว ACG: พท.สามเหลี่ยมเหลือง BCG= ด้านเขียว AF: ด้านเหลือง BF"

จากรูป
สามเหลี่ยมเขียวใหญ่ ACF กับ สามเหลี่ยมเหลืองใหญ่ BCF มีความสูงเท่ากัน
ดังนั้น
พท. สามเหลี่ยมเขียวใหญ่ ACF : พท.สามเหลี่ยมเหลืองใหญ่ BCF
= ด้านเขียว AF : ด้านเหลือง BF
ทำนองเดียวกัน
สามเหลี่ยมเขียวอ่อน AGF กับ สามเหลี่ยมเหลืองอ่อน BGF มีความสูงเท่ากัน
ดังนั้น
สามเหลี่ยมเขียวอ่อน AGF : สามเหลี่ยมเหลืองอ่อน BGF
= ด้านเขียว AF : ด้านเหลือง BF
แต่ พท.เขียว ACG = พท.เขียวใหญ่ ACF - พท.เขียวอ่อน AGF
และ พท.เหลือง BCG = พท.เหลืองใหญ่ BCF - พท.เหลืองอ่อน BGF
ดังนั้น
--------------------------------------------------------------------
พท.เขียว ACG : พท.เหลือง BCG = ด้านเขียว : ด้านเหลือง
--------------------------------------------------------------------
ส่วนคำถามเหล่านี้ ก็พิสูจน์ทำนองเดียวกัน
>แล้วทำไมเส้นที่เป็นด้านร่วมกันของสามเหลี่ยมย่อย 2 รูปในนั้น
>ถึงยาวเท่ากับขนาด(หรืออัตราส่วนก็ไม่รู้)ของพื้นที่นั้นบวกกัน?
>แล้วทำไมเส้นที่ลากต่อมาตัดด้านเมื่อกี้ ถึงยาวเท่ากับอัตราส่วนของพื้นที่ที่มันลากผ่าน?
แสดงความคิดเห็น




ทำไมเส้นมัธยฐานกับจุด centroid ของสามเหลี่ยม...
-ทำไมเส้นมัธยฐานของสามเหลี่ยม ลากไปแล้วไปตัดจุดๆ เดียวเป็นจุด centroid ได้? ทำไมมันไม่เป็นจุดตัดหลายๆ จุดมั่วๆ ?
-ทำไมอัตราส่วนถึงเป็น 2:1 ? ทำไมมันไม่เป็นอย่างอื่น? แถมทำไมมันเป็น 2:1 คงที่ซะด้วย?
-แล้วทำไมเส้นมัธยฐานถึงแบ่งพื้นที่สามเหลี่ยมเป็น 3 ส่วนเท่ากันพอดี?
-ถ้าลากเส้นจากมุมของสามเหลี่ยมทั้ง 3 มาตัดกันที่จุดๆ นึง แล้วลากต่อไปจนถึงด้านตรงข้ามมุมนั้น ทำไมมันถึงแบ่งด้านนั้นๆ ด้วยความยาว-(หรืออัตราส่วนก็ไม่รู้) เท่ากับอัตราส่วนของพื้นที่ที่ไม่ติดกับเส้นนั้นๆ? แล้วทำไมเส้นที่เป็นด้านร่วมกันของสามเหลี่ยมย่อย 2 รูปในนั้น ถึงยาวเท่ากับขนาด(หรืออัตราส่วนก็ไม่รู้)ของพื้นที่นั้นบวกกัน? แล้วทำไมเส้นที่ลากต่อมาตัดด้านเมื่อกี้ ถึงยาวเท่ากับอัตราส่วนของพื้นที่ที่มันลากผ่าน?
-แล้วทำไมเวลาเอาผลรวมของพิกัดจุดที่คูณกับอัตราส่วนพื้นที่ตรงข้ามจุดนั้นๆ มาหารด้วยผลรวมของอัตราส่วนพื้นที่ทั้งหมด จะได้พิกัดของ จุดตัดตรงนั้น? เช่น (x,y) = [4*(15,2) + 2*(6,16) + 3*(-3,4)]/9 = [(60,8)+(12,32)+(-9,12)]/9 = (63,52)/9 = (7, 52/9)
(อธิบายมึนๆ ดูรูปละกัน)
ขอคำอธิบายนอกจากการลองวาดรูปแล้วใช้ตามองว่ามันเป็นอย่างที่มันเป็นหน่อย
ขอบคุณ