สมัยนี้ ม.ปลาย เรียนโหดมาก  เมื่อ 10 กว่าปีก่อน  ผมเรียนโจทย์นี้ในวิชาแคลคูลัส 1 ระดับ ป.ตรี ปี 1

สรุปเนื้อหาแคลคูลัสเบื้องต้น ม.6
https://www.youtube.com/live/Z7_9HmiQH8A?feature=share

คุณสมบัติของเลขยกกำลัง
[Spoil] คลิกเพื่อดูข้อความที่ซ่อนไว้
สูตรการดิฟและการอินทิเกรตฟังก์ชันต่างๆ
(สูตรบางส่วนเกินระดับ ม.6)
[Spoil] คลิกเพื่อดูข้อความที่ซ่อนไว้
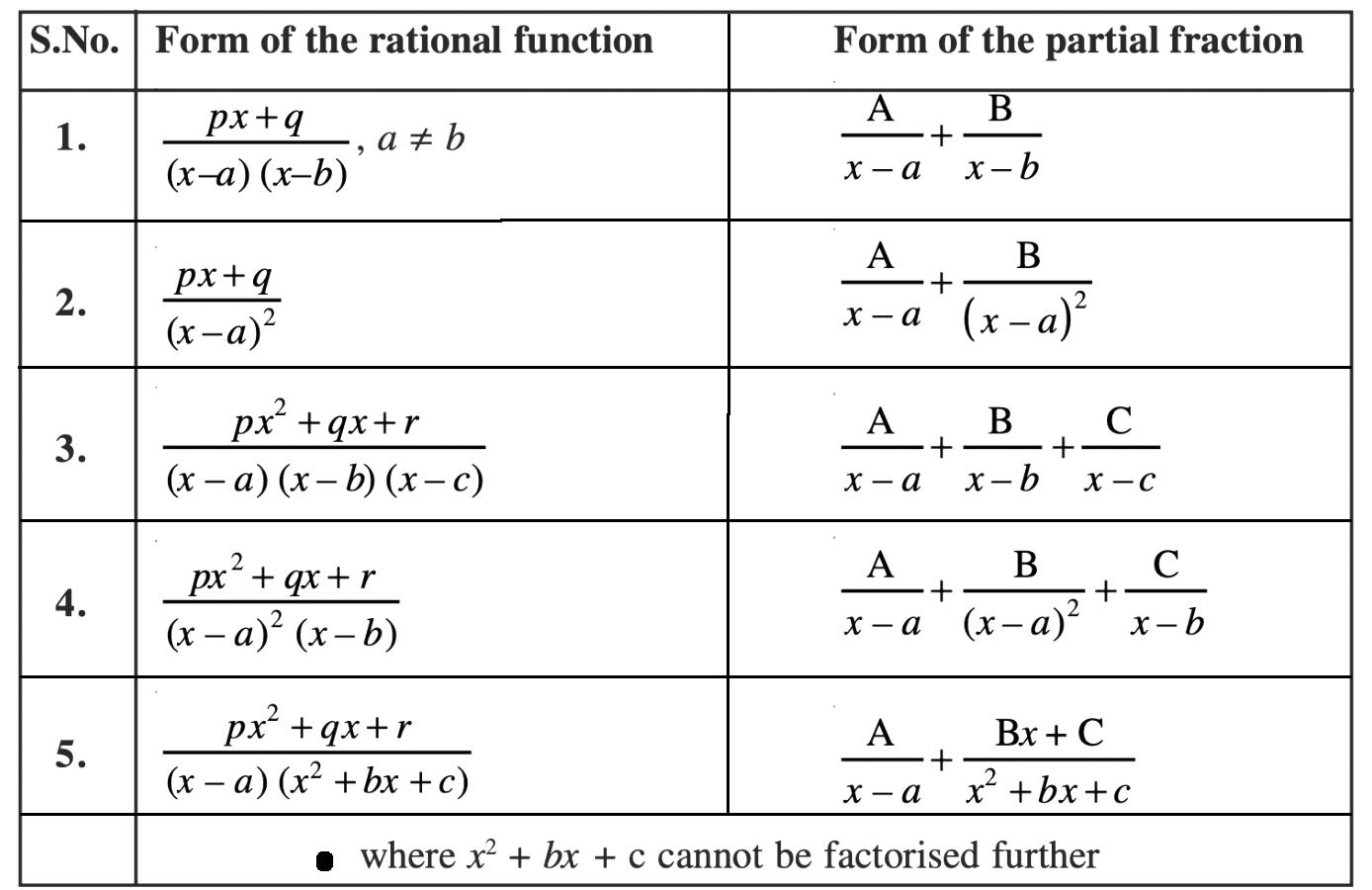
เศษส่วนย่อย (Partial fractions)
[Spoil] คลิกเพื่อดูข้อความที่ซ่อนไว้
∫ f(x) dx = ∫ (e^(2x) + 3e^x) / (e^x + 1)² dx
ใช้วิธีอินทีเกรตโดยการแทนค่าตัวแปร ( Integration by substitution ) , คุณสมบัติของเลขยกกำลัง และเศษส่วนย่อย (partial fractions) 

∫ (e^(2x) + 3e^x) / (e^x + 1)² dx
= ∫ e^x ( (e^x + 3) / (e^x + 1)² ) dx
สมมติตัวแปร u = e^x + 1 , du/dx = e^x จะได้ du = e^x dx
= ∫ (u+2) / u² du
= ∫ 1/u + 2/u² du
= ∫ 1/u du + 2 ∫ 1/u² du
= ∫ 1/u du + 2 ∫ u^(-2) du
= ln IuI + 2(-1/u) + C
= ln IuI - 2/u + C
= ln I e^x + 1 I - 2/( e^x +1 ) + C

_______________________________________

∫ f(x) dx = ∫ sin³x dx
ใช้วิธีอินทีเกรตโดยการแทนค่าตัวแปร ( Integration by substitution ) และเอกลักษณ์ตรีโกณมิติ

∫ sin³x dx
= ∫ sin²x sin x dx
เอกลักษณ์ตรีโกณมิติ sin² x = 1 - cos² x
= ∫ (1 - cos²x)sin x dx
สมมติตัวแปร u = cos x  , du/dx = - sin x  จะได้ du = - sin x dx
= ∫ - (1 - u²) du
= ∫ -1 + u² du
= - ∫ 1 du + ∫ u² du
= - u + u³/3 + C
= - cos x + (cos³ x)/3 + C

ปล. C คือค่าคงที่