ใช้ความรู้เรื่องทฤษฎีจำนวนเบื้องต้นกับเซต
n(U) = (100-0)/2 ปัดเศษลง +1 จะได้จำนวนคู่ตั้งแต่ 0-100 คือ 51 จำนวน
n(A) =  (100-0)/(2×3) ปัดเศษลง +1 จะได้จำนวนคู่ตั้งแต่ 0-100 ที่หารด้วย 3 ลงตัว คือ 17 จำนวน
n(B) =  (100-0)/4 ปัดเศษลง +1 จะได้จำนวนคู่ตั้งแต่ 0-100 ที่หารด้วย 4 ลงตัว คือ 26 จำนวน
n(C) =  (100-0)/(2×5) ปัดเศษลง +1  จะได้จำนวนคู่ตั้งแต่ 0-100 ที่หารด้วย 5 ลงตัว คือ 11 จำนวน

n(A∩B) = (100-0)/(3×4) ปัดเศษลง +1  จะได้จำนวนคู่ตั้งแต่ 0-100 ที่หารด้วย 3 และ 4 ลงตัว คือ 9 จำนวน
n(A∩C) = (100-0)/(2×3×5) ปัดเศษลง +1  จะได้จำนวนคู่ตั้งแต่ 0-100 ที่หารด้วย 3 และ 5 ลงตัว คือ 4 จำนวน
n(B∩C) = (100-0)/(4×5) ปัดเศษลง +1 จะได้จำนวนคู่ตั้งแต่ 0-100 ที่หารด้วย 4 และ 5 ลงตัว คือ 6 จำนวน
n(A∩B∩C) = (100-0)/(3×4×5) ปัดเศษลง +1 จะได้จำนวนคู่ตั้งแต่ 0-100 ที่หารด้วย 3,4 และ5 ลงตัว คือ 2 จำนวน  

ปล. สาเหตุที่ +1 เพราะต้องนับเลขศูนย์รวมไปด้วย เลขศูนย์เป็นจำนวนคู่

แผนภาพเวนน์ออยเลอร์ 3 เซต ตามที่โจทย์บอก
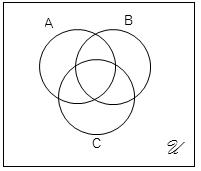1) n(BUC') = n(B∩C)+n(C') = n(B∩C)+(n(U)-n(C))
2) n(A∩B∩C') = n(A∩B) - n(A∩B∩C)
3) n(AUBUC) = n(A)+n(B)+n(C)-n(A∩B)-n(A∩C)-n(B∩C)+n(A∩B∩C)
4) n((AUBUC)') = n(U) - n(AUBUC)