ถ้ามีเกมอยู่เกมนึง โอกาสชนะและแพ้เท่าๆกันคือ 50% : 50% โดยที่ถ้าคุณชนะ คุณจะได้ รางวัลเป็นเงิน 60% ของเงินพนัน แต่หากคุณแพ้ คุณจะต้องเสียเงิน 50% ของเงินพนัน
ถ้าเรามองจาก expectancy แล้ว .5 x +60% + .5 x -50% = +5%
เกมนี้มีมูลค่า +5% หมายความว่าเราควรเล่นเกมนี้ใช่หรือไม่???
ถ้าเรามีเงินอยู่ 1000 บาท เราวางเงินทั้งหมดในเกมนี้ ผลที่ได้คือ
50% ชนะ ได้เงิน 600 บาท 50% แพ้ เสียเงิน 500 บาท
คำถามคือ ถ้าเราเล่นเกมนี้ไปเรื่อยๆด้วยเงื่อนไขเดิมล่ะ
สมมติเราเล่นไป n ครั้ง ชนะ h ครั้ง ท้ายสุดเราก็จะมีเงินเหลือ
=1000((1+60%)^h x (1-50%)^(n-h))
สมมติ h มีค่าประมาณ n/2 เพราะโอกาสคือ 50%
=1000(1.6^(n/2) x .5^(n/2))
=1000(.8^(n/2))
หมายความว่า เกมนี้ ยิ่งเล่นยิ่งจนใช่หรือไม่?
เพราะอะไร ทั้งๆที่เกมนี้ให้ positive expectancy?
หากเราเปลี่ยนเงื่อนไข เป็นการเล่นด้วยเงินเพียงครั้งละ 20% ของเงินที่มีล่ะ
สมมติเราเล่นไป n ครั้ง ออกหัว h ครั้ง ท้ายสุดเราก็จะมีเงินเหลือ
=1000((1+.2x60%)^h x (1-.2x50%)^(n-h))
สมมติ h มีค่าประมาณ n/2 เพราะโอกาสคือ 50%
=1000(1.12^(n/2) x .9^(n/2))
=1000(1.008^(n/2))
คำนวน expectancy = .5 x + .2 x 60% + .5 x - .2 x 50% = +1%
พอเราเล่นน้อยลง เกมนี้ กลับให้ผลตอบแทนที่ดีในระยะยาว
ทั้งที่ expectancy ลดลงน้อยกว่าเกมแรก นั่นคือลดจาก +5% เป็น +.1% เพราะเราเล่นน้อยลง
เกมเดียวกัน แต่เปลี่ยนวิธีการเล่น กลับให้ผลที่แตกต่างกันโดยสิ้นเชิง เพราะอะไรกัน
ทั้งที่ expectancy น้อยกว่า แต่กลับให้ ความมั่งคั่งสุดท้ายสูงกว่า
คำตอบก็คือ เพราะความมั่งคั่งของเรา มีลักษณะเป็นการทบต้น นั่นคือการคูณไม่ใช่การบวก
สิ่งที่เราต้องการคือความมั่งคั่งสุดท้ายสูงสุด แล้วเราควรทำอย่างไร
expectancy ไม่ใช่แนวคิดที่ผิด แต่มุมมองที่บิดเบือนต่างหากเป็นสิ่งที่ผิด
เราทุกคน พยายามที่จะแสวงหากำไรสูงสุด นั่นคือ ค่าคาดหวังสูงสุด
แต่ความมั่งคั่งของเรา เป็นลักษณะทบต้น นั่นคือ
Wn = Wo x (1 + R1) x (1 + R2) x (1 + R3) x ... x (1 + Rn)
แต่ expectancy คือ

ซึ่งมีความเป็น linearity ดังนั้น หากเราต้องการนำค่าคาดหวังมาใช้ เราต้องมองหาส่วนที่มีความเป็น linerity ของ wealth นั่นคือ
Wn = Wo x (1 + R1) x (1 + R2) x (1 + R3) x ... x (1 + Rn)
= Wo x exp( ln(1 + R1) ) x exp( ln(1 + R2) ) x exp( ln(1 + R3) ) x ... x exp( ln(1 + Rn) )
= Wo x exp( ln(1 + R1) + ln(1 + R2) + ln(1 + R3) + ... + ln(1 + Rn) )
นั้นคือ ส่วนของ exp( ln(1 + R1) + ln(1 + R2) + ln(1 + R3) + ... + ln(1 + Rn) ) นั่นเอง
ดังนั้น หากเราใช้
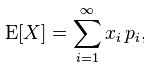
เราก็จะได้ค่า expectancy ซึ่งผิดกับจุดประสงค์ที่ต้องการให้ความมั่งคั่งสุดท้ายสูงสุด
แต่เราควรทำคือ เปลี่ยน X จาก R เป็น ln(1+R) เพื่อให้ mathematically agree และสอดคล้องกับจุดประสงค์ดังกล่าว นั่นคือ
ในเกมที่เรา แทงหมดหน้าตัก
E(X) = .5 x ln(1.6) + .5 x ln(.5)
= .5 x ln(.8) ซึ่งน้อยกว่า 0
ในขณะที่เกมที่เราแทง 20%
E(X) = .5 x ln(1.12) + .5 x ln(.9)
=.5 x ln(1.008) ซึ่งให้ค่าบวก
จะให้มุมมองที่ตรงตามความจริง และตอบโจทย์ความต้องการความมั่งคั่งสูงสุดได้ตรงประเด็นกว่า
ดังนั้น การใช้ expectancy ไม่ใช่สิ่งผิด แต่สิ่งที่ผิดคือ การใช้ expectancy กับตัวแปรที่ผิด เพราะความมั่งคั่งของเรา มีลักษณะทบต้น เราไม่สามารถ treat ความมั่งคั้งของเราแบบ linearity ได้ เพราะหากเราทำเช่นนั้น เมื่อ W ลดลงจนเป็น 0 เราจะไม่เหลือเงินต้นไว้ต่อยอด คือหมดตัวนั่นเอง
หากเปรียบเหตุการณ์ข้างต้นกับ utility แล้ว นั่นก็คือ เราพยายาม maximize utility แบบ log utility function นั่นเอง

Expectancy กับมุมมองที่บิดเบือนในการลงทุน
ถ้าเรามองจาก expectancy แล้ว .5 x +60% + .5 x -50% = +5%
เกมนี้มีมูลค่า +5% หมายความว่าเราควรเล่นเกมนี้ใช่หรือไม่???
ถ้าเรามีเงินอยู่ 1000 บาท เราวางเงินทั้งหมดในเกมนี้ ผลที่ได้คือ
50% ชนะ ได้เงิน 600 บาท 50% แพ้ เสียเงิน 500 บาท
คำถามคือ ถ้าเราเล่นเกมนี้ไปเรื่อยๆด้วยเงื่อนไขเดิมล่ะ
สมมติเราเล่นไป n ครั้ง ชนะ h ครั้ง ท้ายสุดเราก็จะมีเงินเหลือ
=1000((1+60%)^h x (1-50%)^(n-h))
สมมติ h มีค่าประมาณ n/2 เพราะโอกาสคือ 50%
=1000(1.6^(n/2) x .5^(n/2))
=1000(.8^(n/2))
หมายความว่า เกมนี้ ยิ่งเล่นยิ่งจนใช่หรือไม่?
เพราะอะไร ทั้งๆที่เกมนี้ให้ positive expectancy?
หากเราเปลี่ยนเงื่อนไข เป็นการเล่นด้วยเงินเพียงครั้งละ 20% ของเงินที่มีล่ะ
สมมติเราเล่นไป n ครั้ง ออกหัว h ครั้ง ท้ายสุดเราก็จะมีเงินเหลือ
=1000((1+.2x60%)^h x (1-.2x50%)^(n-h))
สมมติ h มีค่าประมาณ n/2 เพราะโอกาสคือ 50%
=1000(1.12^(n/2) x .9^(n/2))
=1000(1.008^(n/2))
คำนวน expectancy = .5 x + .2 x 60% + .5 x - .2 x 50% = +1%
พอเราเล่นน้อยลง เกมนี้ กลับให้ผลตอบแทนที่ดีในระยะยาว
ทั้งที่ expectancy ลดลงน้อยกว่าเกมแรก นั่นคือลดจาก +5% เป็น +.1% เพราะเราเล่นน้อยลง
เกมเดียวกัน แต่เปลี่ยนวิธีการเล่น กลับให้ผลที่แตกต่างกันโดยสิ้นเชิง เพราะอะไรกัน
ทั้งที่ expectancy น้อยกว่า แต่กลับให้ ความมั่งคั่งสุดท้ายสูงกว่า
คำตอบก็คือ เพราะความมั่งคั่งของเรา มีลักษณะเป็นการทบต้น นั่นคือการคูณไม่ใช่การบวก
สิ่งที่เราต้องการคือความมั่งคั่งสุดท้ายสูงสุด แล้วเราควรทำอย่างไร
expectancy ไม่ใช่แนวคิดที่ผิด แต่มุมมองที่บิดเบือนต่างหากเป็นสิ่งที่ผิด
เราทุกคน พยายามที่จะแสวงหากำไรสูงสุด นั่นคือ ค่าคาดหวังสูงสุด
แต่ความมั่งคั่งของเรา เป็นลักษณะทบต้น นั่นคือ
Wn = Wo x (1 + R1) x (1 + R2) x (1 + R3) x ... x (1 + Rn)
แต่ expectancy คือ
ซึ่งมีความเป็น linearity ดังนั้น หากเราต้องการนำค่าคาดหวังมาใช้ เราต้องมองหาส่วนที่มีความเป็น linerity ของ wealth นั่นคือ
Wn = Wo x (1 + R1) x (1 + R2) x (1 + R3) x ... x (1 + Rn)
= Wo x exp( ln(1 + R1) ) x exp( ln(1 + R2) ) x exp( ln(1 + R3) ) x ... x exp( ln(1 + Rn) )
= Wo x exp( ln(1 + R1) + ln(1 + R2) + ln(1 + R3) + ... + ln(1 + Rn) )
นั้นคือ ส่วนของ exp( ln(1 + R1) + ln(1 + R2) + ln(1 + R3) + ... + ln(1 + Rn) ) นั่นเอง
ดังนั้น หากเราใช้
เราก็จะได้ค่า expectancy ซึ่งผิดกับจุดประสงค์ที่ต้องการให้ความมั่งคั่งสุดท้ายสูงสุด
แต่เราควรทำคือ เปลี่ยน X จาก R เป็น ln(1+R) เพื่อให้ mathematically agree และสอดคล้องกับจุดประสงค์ดังกล่าว นั่นคือ
ในเกมที่เรา แทงหมดหน้าตัก
E(X) = .5 x ln(1.6) + .5 x ln(.5)
= .5 x ln(.8) ซึ่งน้อยกว่า 0
ในขณะที่เกมที่เราแทง 20%
E(X) = .5 x ln(1.12) + .5 x ln(.9)
=.5 x ln(1.008) ซึ่งให้ค่าบวก
จะให้มุมมองที่ตรงตามความจริง และตอบโจทย์ความต้องการความมั่งคั่งสูงสุดได้ตรงประเด็นกว่า
ดังนั้น การใช้ expectancy ไม่ใช่สิ่งผิด แต่สิ่งที่ผิดคือ การใช้ expectancy กับตัวแปรที่ผิด เพราะความมั่งคั่งของเรา มีลักษณะทบต้น เราไม่สามารถ treat ความมั่งคั้งของเราแบบ linearity ได้ เพราะหากเราทำเช่นนั้น เมื่อ W ลดลงจนเป็น 0 เราจะไม่เหลือเงินต้นไว้ต่อยอด คือหมดตัวนั่นเอง
หากเปรียบเหตุการณ์ข้างต้นกับ utility แล้ว นั่นก็คือ เราพยายาม maximize utility แบบ log utility function นั่นเอง